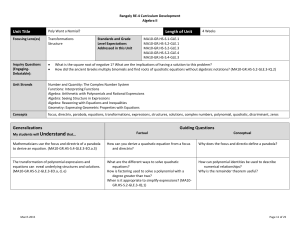
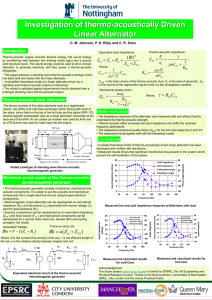
Document
... ◦ Squarewave - easier to work with ◦ Four Phases for the Channel Select ◦ Frequency error also divided down ...
... ◦ Squarewave - easier to work with ◦ Four Phases for the Channel Select ◦ Frequency error also divided down ...
Fibonacci Extended
... After calculating each set in Excel, I found a distinct relationship between the sum of the terms and the 7th term. I found that in each set, the sum of the terms divided by the 7th term always equaled 11. After reading about the Fibonacci numbers, I found that the number 11 is called the golden st ...
... After calculating each set in Excel, I found a distinct relationship between the sum of the terms and the 7th term. I found that in each set, the sum of the terms divided by the 7th term always equaled 11. After reading about the Fibonacci numbers, I found that the number 11 is called the golden st ...
PDF
... is not divisible by the integer n, can be decomposed to a sum of partial fractions as follows: m m1 m2 mt = ν1 + ν2 + · · · + νt n p1 p2 pt Here, the pi ’s are distinct positive prime numbers, the νi ’s positive integers and the mi ’s some integers. Cf. the partial fractions of expressions. Examples ...
... is not divisible by the integer n, can be decomposed to a sum of partial fractions as follows: m m1 m2 mt = ν1 + ν2 + · · · + νt n p1 p2 pt Here, the pi ’s are distinct positive prime numbers, the νi ’s positive integers and the mi ’s some integers. Cf. the partial fractions of expressions. Examples ...
FE Exam Review - Mathematics - Biosystems and Agricultural
... Logarithms • Think of logarithms as exponents... bc x – Exponent is c and expression above is the logarithm of x to the base b log b ( x) c b c x – Base for common logs is 10 (log=log10) – Base for natural logs is e (ln=loge), e = 2.71828 ...
... Logarithms • Think of logarithms as exponents... bc x – Exponent is c and expression above is the logarithm of x to the base b log b ( x) c b c x – Base for common logs is 10 (log=log10) – Base for natural logs is e (ln=loge), e = 2.71828 ...
MATH 120 chapter 3 online quiz
... first car travels at 60 m.p.h. while the second travels at 70 m.p.h. In how many hours will they be 600 miles apart? a) d - 600 = 60t and d+600 =70t b) d = 60 t + 70 and d=600 - 70t c) d =60t and 600 - d = 70t * d) d = t +10 and 10d =60 7. Which of the following systems could be used to solve the f ...
... first car travels at 60 m.p.h. while the second travels at 70 m.p.h. In how many hours will they be 600 miles apart? a) d - 600 = 60t and d+600 =70t b) d = 60 t + 70 and d=600 - 70t c) d =60t and 600 - d = 70t * d) d = t +10 and 10d =60 7. Which of the following systems could be used to solve the f ...
Derivation of the BLOSUM substitution matrices:
... A pioneer in this field was Margaret Dayhoff, who created the PAM (Per cent Accepted point Mutations) substitution matrices. She used sets of closely related sequences to model how evolution occurs over short distances, and then extrapolated these findings to longer evolutionary distances. The other ...
... A pioneer in this field was Margaret Dayhoff, who created the PAM (Per cent Accepted point Mutations) substitution matrices. She used sets of closely related sequences to model how evolution occurs over short distances, and then extrapolated these findings to longer evolutionary distances. The other ...
Mathematics of radio engineering

The mathematics of radio engineering is the mathematical description by complex analysis of the electromagnetic theory applied to radio. Waves have been studied since ancient times and many different techniques have developed of which the most useful idea is the superposition principle which apply to radio waves. The Huygen's principle, which says that each wavefront creates an infinite number of new wavefronts that can be added, is the base for this analysis.