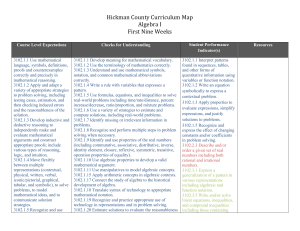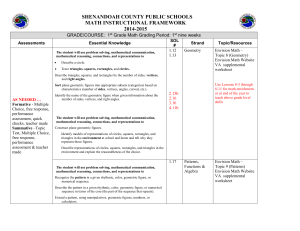
Inside Algebra Correlated to the New Jersey Student Learning
... describe numerical relationships. For example, the polynomial identity (x2 + y2)2 = (x2 – y2)2 +(2xy)2 ...
... describe numerical relationships. For example, the polynomial identity (x2 + y2)2 = (x2 – y2)2 +(2xy)2 ...
CIRCULAR (TRIGONOMETRIC) FUNCTIONS RECIPROCAL
... The graphs of y = cosec( x) , y = sec( x ) and y = cot( x ) can be derived by using the theory of reciprocals. Simply plot the reciprocal of each value of y at select values of x . Note that the X intercepts on the graphs of y = sin( x ) , y = cos( x ) and y = tan( x ) become vertical asymptotes on ...
... The graphs of y = cosec( x) , y = sec( x ) and y = cot( x ) can be derived by using the theory of reciprocals. Simply plot the reciprocal of each value of y at select values of x . Note that the X intercepts on the graphs of y = sin( x ) , y = cos( x ) and y = tan( x ) become vertical asymptotes on ...
Topological aspects of real-valued logic
... this approach). Recently there has been a considerable amount of activity in a [0, 1]-valued logic called continuous first-order logic, introduced by Ben Yaacov and Usvyatsov [16]. Continuous first-order logic is a reformulation of Henson’s logic in the framework of Chang and Keisler, and is the bas ...
... this approach). Recently there has been a considerable amount of activity in a [0, 1]-valued logic called continuous first-order logic, introduced by Ben Yaacov and Usvyatsov [16]. Continuous first-order logic is a reformulation of Henson’s logic in the framework of Chang and Keisler, and is the bas ...
Let me begin by reminding you of a number of passages ranging
... If these remarks do not explicitly contradict Frege’s earlier claims, then, at the very least, they raise serious interpretive difficulties about how we are to reconcile them with the various truth oriented pronouncement concerning the goal, the task, the aim, and essence of logic that Frege makes b ...
... If these remarks do not explicitly contradict Frege’s earlier claims, then, at the very least, they raise serious interpretive difficulties about how we are to reconcile them with the various truth oriented pronouncement concerning the goal, the task, the aim, and essence of logic that Frege makes b ...