Review: complex numbers
... Every non-zero complex number has two square roots, which are opposites of each other. For example, (2 – 3i)2 = –5 – 12i and (–2 + 3i)2 = –5 – 12i. ...
... Every non-zero complex number has two square roots, which are opposites of each other. For example, (2 – 3i)2 = –5 – 12i and (–2 + 3i)2 = –5 – 12i. ...
An Example of Induction: Fibonacci Numbers
... This short document is an example of an induction proof. Our goal is to rigorously prove something we observed experimentally in class, that every fifth Fibonacci number is a multiple of 5. As usual in mathematics, we have to start by carefully defining the objects we are studying. Definition. The s ...
... This short document is an example of an induction proof. Our goal is to rigorously prove something we observed experimentally in class, that every fifth Fibonacci number is a multiple of 5. As usual in mathematics, we have to start by carefully defining the objects we are studying. Definition. The s ...
CARLOS AUGUSTO DI PRISCO The notion of infinite appears in
... The notion of infinite appears in mathematics in many different ways. The notion of limit or endless processes of approximations have been considered since ancient times, but it was in the decade of 1870 that the systematic study of infinite collections as completed totalities was initiated by Georg ...
... The notion of infinite appears in mathematics in many different ways. The notion of limit or endless processes of approximations have been considered since ancient times, but it was in the decade of 1870 that the systematic study of infinite collections as completed totalities was initiated by Georg ...
Evaluating the exact infinitesimal values of area of Sierpinski`s
... Due to this declared applied statement, such concepts as bijection, numerable and continuum sets, cardinal and ordinal numbers cannot be used in this paper because they belong to the theories working with different assumptions. As a consequence, the new approach is different also with respect to the ...
... Due to this declared applied statement, such concepts as bijection, numerable and continuum sets, cardinal and ordinal numbers cannot be used in this paper because they belong to the theories working with different assumptions. As a consequence, the new approach is different also with respect to the ...
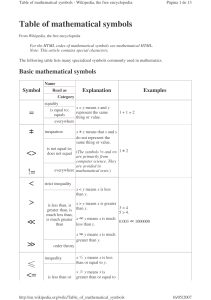
Table of mathematical symbols
... inner product of x and y The standard inner product between two as defined in an inner vectors x = (2, 3) and y = (−1, 5) is: ...
... inner product of x and y The standard inner product between two as defined in an inner vectors x = (2, 3) and y = (−1, 5) is: ...
Computer Science at Oxford
... find the hcf more quickly (this kind of technique is called fusion). Could use prime numbers. ...
... find the hcf more quickly (this kind of technique is called fusion). Could use prime numbers. ...