
Differential geometric formulation of Maxwell`s equations
... Here the 2-forms E and B encode those entries of matrix F that correspond to the electric and magnetic field, respectively. Note that the matrix representation of vectors E and B in Equation (11) is redundant, since each entry appears twice (in particular, F is skewsymmetric). However, Equations (13 ...
... Here the 2-forms E and B encode those entries of matrix F that correspond to the electric and magnetic field, respectively. Note that the matrix representation of vectors E and B in Equation (11) is redundant, since each entry appears twice (in particular, F is skewsymmetric). However, Equations (13 ...
Lecture 15: Projections onto subspaces
... Figure 1: The point closest to b on the line determined by a. We can see from Figure 1 that this closest point p is at the intersection formed by a line through b that is orthogonal to a. If we think of p as an approximation of b, then the length of e = b − p is the error in that approxi mation. We ...
... Figure 1: The point closest to b on the line determined by a. We can see from Figure 1 that this closest point p is at the intersection formed by a line through b that is orthogonal to a. If we think of p as an approximation of b, then the length of e = b − p is the error in that approxi mation. We ...
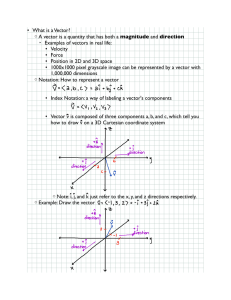
VECTORS C4 Worksheet C
... Find the value of the constants a and b such that line r = 3i − 5j + k + λ(2i + aj + bk) a passes through the point (9, −2, −8), b is parallel to the line r = 4j − 2k + µ(8i − 4j + 2k). ...
... Find the value of the constants a and b such that line r = 3i − 5j + k + λ(2i + aj + bk) a passes through the point (9, −2, −8), b is parallel to the line r = 4j − 2k + µ(8i − 4j + 2k). ...
Vector geometry (v2) R2,R3
... we have vector b, and vector a which is not collinear to b. We can view vector a as being composted of some part that is parallel to b, and some part that are orthogonal to b. This is called the projection of a on to (or in the direction of) b. ...
... we have vector b, and vector a which is not collinear to b. We can view vector a as being composted of some part that is parallel to b, and some part that are orthogonal to b. This is called the projection of a on to (or in the direction of) b. ...
Cartesian tensor
In geometry and linear algebra, a Cartesian tensor uses an orthonormal basis to represent a tensor in a Euclidean space in the form of components. Converting a tensor's components from one such basis to another is through an orthogonal transformation.The most familiar coordinate systems are the two-dimensional and three-dimensional Cartesian coordinate systems. Cartesian tensors may be used with any Euclidean space, or more technically, any finite-dimensional vector space over the field of real numbers that has an inner product.Use of Cartesian tensors occurs in physics and engineering, such as with the Cauchy stress tensor and the moment of inertia tensor in rigid body dynamics. Sometimes general curvilinear coordinates are convenient, as in high-deformation continuum mechanics, or even necessary, as in general relativity. While orthonormal bases may be found for some such coordinate systems (e.g. tangent to spherical coordinates), Cartesian tensors may provide considerable simplification for applications in which rotations of rectilinear coordinate axes suffice. The transformation is a passive transformation, since the coordinates are changed and not the physical system.



















![Final Exam [pdf]](http://s1.studyres.com/store/data/008845375_1-2a4eaf24d363c47c4a00c72bb18ecdd2-300x300.png)


