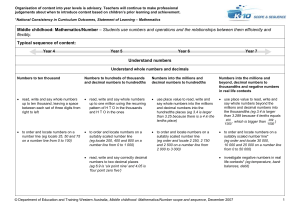
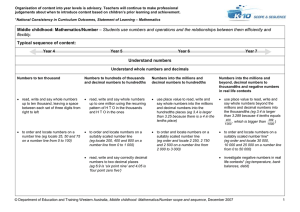
36(4)
... proved by Hartman [3] and Koksma [6]. Recently, the author has shown [1] that the theorem of Uchiyama no longer holds if the constant s214 is replaced by any smaller number. Assuming weaker arithmetical restrictions in (1.2) on numerators and denominators of the approximants, the constant in (1.1) c ...
... proved by Hartman [3] and Koksma [6]. Recently, the author has shown [1] that the theorem of Uchiyama no longer holds if the constant s214 is replaced by any smaller number. Assuming weaker arithmetical restrictions in (1.2) on numerators and denominators of the approximants, the constant in (1.1) c ...
On the Sum of Corresponding Factorials and Triangular Numbers
... polite number is defined as a positive integer that can be written as the sum of two or more consecutive positive integers and if all numbers in the sum are strictly greater than 1, the polite number is also called trapezoidal number because it represents pattern of points arranged in a trapezoid [4 ...
... polite number is defined as a positive integer that can be written as the sum of two or more consecutive positive integers and if all numbers in the sum are strictly greater than 1, the polite number is also called trapezoidal number because it represents pattern of points arranged in a trapezoid [4 ...
pdf file
... algebra) that a student encounters, in which one truly has to grapple with the subtleties of a truly rigourous mathematical proof. As such, the course offers an excellent chance to go back to the foundations of mathematics - and in particular, the construction of the real numbers - and do it properl ...
... algebra) that a student encounters, in which one truly has to grapple with the subtleties of a truly rigourous mathematical proof. As such, the course offers an excellent chance to go back to the foundations of mathematics - and in particular, the construction of the real numbers - and do it properl ...
Full text
... A Fibonacci expansion of a nonnegative integer n is an expression of n as a sum of Fibonacci numbers Fk with k > 2. It may be thought of as a partition of n into Fibonacci parts. The most commonly studied such expansion is the unique one in which the parts are all distinct and no two consecutive Fib ...
... A Fibonacci expansion of a nonnegative integer n is an expression of n as a sum of Fibonacci numbers Fk with k > 2. It may be thought of as a partition of n into Fibonacci parts. The most commonly studied such expansion is the unique one in which the parts are all distinct and no two consecutive Fib ...
A Readable Introduction to Real Mathematics
... [Hint: If p1 , p2 , . . . , pn are n such primes, show that (4 · p1 · p2 · · · pn ) − 1 has at least one prime divisor of the given form.] Answer: We first prove the equivalent statement for primes of the form 4k + 3 where k is any nonnegative integer (thus including the case k = 0). Since 4 · 1 + 3 ...
... [Hint: If p1 , p2 , . . . , pn are n such primes, show that (4 · p1 · p2 · · · pn ) − 1 has at least one prime divisor of the given form.] Answer: We first prove the equivalent statement for primes of the form 4k + 3 where k is any nonnegative integer (thus including the case k = 0). Since 4 · 1 + 3 ...
NUMBER SETS Jaroslav Beránek Brno 2013 Contents Introduction
... (A1) For each element x of the set P there exists its successor, which will be denoted x\.. (A2) In the set P there exists an element e P, which is not a successor of any element of the set P. (A3) Different elements have different successors. (A4) Full Induction Axiom. Let M P. If there applies: ...
... (A1) For each element x of the set P there exists its successor, which will be denoted x\.. (A2) In the set P there exists an element e P, which is not a successor of any element of the set P. (A3) Different elements have different successors. (A4) Full Induction Axiom. Let M P. If there applies: ...
Infinity

Infinity (symbol: ∞) is an abstract concept describing something without any limit and is relevant in a number of fields, predominantly mathematics and physics.In mathematics, ""infinity"" is often treated as if it were a number (i.e., it counts or measures things: ""an infinite number of terms"") but it is not the same sort of number as natural or real numbers. In number systems incorporating infinitesimals, the reciprocal of an infinitesimal is an infinite number, i.e., a number greater than any real number; see 1/∞.Georg Cantor formalized many ideas related to infinity and infinite sets during the late 19th and early 20th centuries. In the theory he developed, there are infinite sets of different sizes (called cardinalities). For example, the set of integers is countably infinite, while the infinite set of real numbers is uncountable.