Natural Numbers: The counting numbers starting at 1: {1, 2, 3,
... numbers either stop or repeat. For example, ½ = 0.5 (stops), 1/3 = 0.33333… (repeats), 1/4 = 0.25 (stops), 1/5 = 0.2 (stops), 1/6 = 0.166666… (repeats), 6/2 = 3 (stops), 60/4 = 15 (stops), etc. Irrational numbers, : Irrational numbers are all the numbers that can’t be written as a ratio of two integ ...
... numbers either stop or repeat. For example, ½ = 0.5 (stops), 1/3 = 0.33333… (repeats), 1/4 = 0.25 (stops), 1/5 = 0.2 (stops), 1/6 = 0.166666… (repeats), 6/2 = 3 (stops), 60/4 = 15 (stops), etc. Irrational numbers, : Irrational numbers are all the numbers that can’t be written as a ratio of two integ ...
Infinite numbers: what are they and what are they good for?
... then P(n) is true for all natural numbers n. Using these axioms, we can develop virtually all mathematics that does not involve infinite sets in an essential way, for example most of number theory, including the Prime Number Theorem. There is even a serious claim that Wiles’s proof of Fermat’s Last ...
... then P(n) is true for all natural numbers n. Using these axioms, we can develop virtually all mathematics that does not involve infinite sets in an essential way, for example most of number theory, including the Prime Number Theorem. There is even a serious claim that Wiles’s proof of Fermat’s Last ...
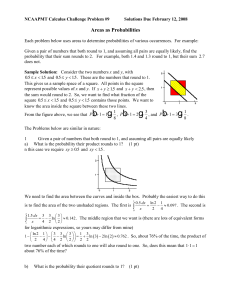
Discrete Math, Spring 2013 - Some Sample Problems
... 3. Prove that for any real numbers x and y if x + y ≥ 2 then x ≥ 1 or y ≥ 1. 4. For any set S, recall that P(S) denotes the set of all subsets of S. a. List the elements of P(P({∅})). b. How many elements does P(P(P({∅}))) have? c. List the elements of P(P(P({∅}))). 5. Let S and T be sets. a. Show t ...
... 3. Prove that for any real numbers x and y if x + y ≥ 2 then x ≥ 1 or y ≥ 1. 4. For any set S, recall that P(S) denotes the set of all subsets of S. a. List the elements of P(P({∅})). b. How many elements does P(P(P({∅}))) have? c. List the elements of P(P(P({∅}))). 5. Let S and T be sets. a. Show t ...
Infinity

Infinity (symbol: ∞) is an abstract concept describing something without any limit and is relevant in a number of fields, predominantly mathematics and physics.In mathematics, ""infinity"" is often treated as if it were a number (i.e., it counts or measures things: ""an infinite number of terms"") but it is not the same sort of number as natural or real numbers. In number systems incorporating infinitesimals, the reciprocal of an infinitesimal is an infinite number, i.e., a number greater than any real number; see 1/∞.Georg Cantor formalized many ideas related to infinity and infinite sets during the late 19th and early 20th centuries. In the theory he developed, there are infinite sets of different sizes (called cardinalities). For example, the set of integers is countably infinite, while the infinite set of real numbers is uncountable.