WORKSHOP: Matter and Working with Significant Figures
... The following rules apply to determining the number of significant figures in a measured quantity: 1. All NONZERO digits ARE significant: 457 cm (three significant figures) 0.25 g (two significant figures). 2. IMBEDDED ZEROS (between nonzero digits) ARE significant 1005 kg (four significant figures) ...
... The following rules apply to determining the number of significant figures in a measured quantity: 1. All NONZERO digits ARE significant: 457 cm (three significant figures) 0.25 g (two significant figures). 2. IMBEDDED ZEROS (between nonzero digits) ARE significant 1005 kg (four significant figures) ...
Decimals, Fractions and Percentages - KCPE-KCSE
... The decimal point is the most important part of a Decimal Number. It is exactly to the right of the Units position. Without it, we would be lost ... and not know what each position meant. Now we can continue with smaller and smaller values, from tenths, to hundredths, and so on, like in this example ...
... The decimal point is the most important part of a Decimal Number. It is exactly to the right of the Units position. Without it, we would be lost ... and not know what each position meant. Now we can continue with smaller and smaller values, from tenths, to hundredths, and so on, like in this example ...
Summer HHW Class 10 Maths - Kendriya Vidyalaya Bairagarh
... Show that the every positive even integer is of the form2q and every positive odd integer is of the form2q+1where q is some integer. Use Euclid’s division algorithm to find the HCF of a)1288 and 575 b)867 and 255 Prove that is not a rational number. Find the largest positive integer that will divide ...
... Show that the every positive even integer is of the form2q and every positive odd integer is of the form2q+1where q is some integer. Use Euclid’s division algorithm to find the HCF of a)1288 and 575 b)867 and 255 Prove that is not a rational number. Find the largest positive integer that will divide ...
Mathematics
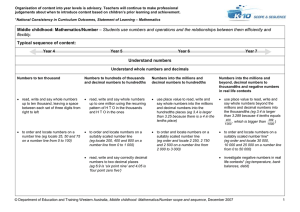
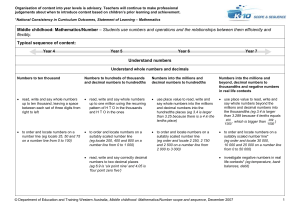
... patterns in the multiples of numbers* (eg multiples of 5 end in 5 or 0) and prime and composite numbers to 20, determining that a prime number has two factors, 1 and the number itself count in tenths* (eg 2.3, 2.4, 2.5) and hundredths for money and measures (eg use the scale on a tape measure to ...
... patterns in the multiples of numbers* (eg multiples of 5 end in 5 or 0) and prime and composite numbers to 20, determining that a prime number has two factors, 1 and the number itself count in tenths* (eg 2.3, 2.4, 2.5) and hundredths for money and measures (eg use the scale on a tape measure to ...
Review Semester 2 with #36-7
... Does the infinite geometric series converge? If so, give the sum. If not, write “does not exist”. ...
... Does the infinite geometric series converge? If so, give the sum. If not, write “does not exist”. ...
Ratios
... In the context of ratios, the word “per” means division. For example, miles per hour. When you properly set up your proportions, you should check that the numerators all have the same units. Also check the denominators to ensure that they have the same units as well. ...
... In the context of ratios, the word “per” means division. For example, miles per hour. When you properly set up your proportions, you should check that the numerators all have the same units. Also check the denominators to ensure that they have the same units as well. ...
Adding and Subtracting Fractions
... • First, we focus on the denominators: 3 & 6. • We need to find the Least Common Denominator. • List on multiples of 3 and 6 until one overlaps. • In this case, it is 6.!12 overlaps but we want the ...
... • First, we focus on the denominators: 3 & 6. • We need to find the Least Common Denominator. • List on multiples of 3 and 6 until one overlaps. • In this case, it is 6.!12 overlaps but we want the ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.