Lesson 2
... Nadia and Peter each take candy from the candy jar. Peter reaches in first and grabs one handful. He gets 7 pieces of candy. Nadia grabs with both hands and gets 7 pieces in one hand and 5 in the other. The following day Peter gets to go first – he grabs with both hands and gets 5 pieces in one hand ...
... Nadia and Peter each take candy from the candy jar. Peter reaches in first and grabs one handful. He gets 7 pieces of candy. Nadia grabs with both hands and gets 7 pieces in one hand and 5 in the other. The following day Peter gets to go first – he grabs with both hands and gets 5 pieces in one hand ...
Set Notation
... Equivalent Sets – contain the same number of elements. Cardinalities are equal: n(A) = n(B) Equal, equivalent, or both? A = {The Graduate, The Godfather, Titanic} B = {Hoffman, Brando, DiCaprio} Not equal – do not contain exactly the same elements Equivalent – each contains three elements: n(A) = n( ...
... Equivalent Sets – contain the same number of elements. Cardinalities are equal: n(A) = n(B) Equal, equivalent, or both? A = {The Graduate, The Godfather, Titanic} B = {Hoffman, Brando, DiCaprio} Not equal – do not contain exactly the same elements Equivalent – each contains three elements: n(A) = n( ...
y6 block e plan - School
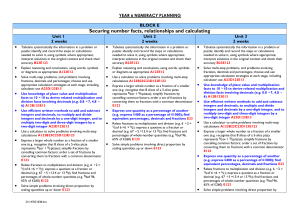
... the calculations needed to solve problems. They interpret solutions in the original context and check their accuracy. They use symbols where appropriate to explain their reasoning and conclusions. Children solve multistep problems by breaking each problem down into steps, identifying and recording t ...
... the calculations needed to solve problems. They interpret solutions in the original context and check their accuracy. They use symbols where appropriate to explain their reasoning and conclusions. Children solve multistep problems by breaking each problem down into steps, identifying and recording t ...
Lecture 5. Introduction to Set Theory and the Pigeonhole Principle
... 3. A set equivalence (or a bijection) if it is both one-to-one and onto. Such functions are also called one-to-one correspondences. Example 2. Again let A = {1, 2, 3} and B = {a, b, c}. Let k = {1, a), (2, b), (3, c)}. The function k is one-to-one because no element of B appears more than once and o ...
... 3. A set equivalence (or a bijection) if it is both one-to-one and onto. Such functions are also called one-to-one correspondences. Example 2. Again let A = {1, 2, 3} and B = {a, b, c}. Let k = {1, a), (2, b), (3, c)}. The function k is one-to-one because no element of B appears more than once and o ...