6th-Grade-Math
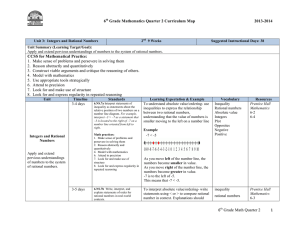
... distance from zero. In terms of absolute value (or distance) the absolute value of –24 is greater than the absolute value of –14. For negative numbers, as the absolute value increases, the value of the negative number decreases. ...
... distance from zero. In terms of absolute value (or distance) the absolute value of –24 is greater than the absolute value of –14. For negative numbers, as the absolute value increases, the value of the negative number decreases. ...
Developing Mathematical Thinking
... We acknowledge with thanks, the work of Bill Norman of the Materials Production Unit of the Open University who prepared the artwork for the modules. Acknowledgement is made to the Cockcroft report [Cockcroft, W. H. (1982) Mathematics counts, London: Her Majesty’s Stationery Office], and to the adva ...
... We acknowledge with thanks, the work of Bill Norman of the Materials Production Unit of the Open University who prepared the artwork for the modules. Acknowledgement is made to the Cockcroft report [Cockcroft, W. H. (1982) Mathematics counts, London: Her Majesty’s Stationery Office], and to the adva ...
Tietze Extension Theorem
... Let f be a real-yielding function, let r be a real number, and let X be a set. We say that f is absolutely bounded by r in X if and only if: (Def. 1) For every set x such that x ∈ X ∩ dom f holds |f (x)| ≤ r. Let us mention that there exists a sequence of real numbers which is summable, constant, an ...
... Let f be a real-yielding function, let r be a real number, and let X be a set. We say that f is absolutely bounded by r in X if and only if: (Def. 1) For every set x such that x ∈ X ∩ dom f holds |f (x)| ≤ r. Let us mention that there exists a sequence of real numbers which is summable, constant, an ...
The Uniform Continuity of Functions on Normed Linear Spaces
... (Def. 2)(i) X ⊆ dom f, and (ii) for every r such that 0 < r there exists s such that 0 < s and for all x1 , x2 such that x1 ∈ X and x2 ∈ X and kx1 − x2 k < s holds |fx1 − fx2 | < r. The following propositions are true: (1) If f is uniformly continuous on X and X1 ⊆ X, then f is uniformly continuous ...
... (Def. 2)(i) X ⊆ dom f, and (ii) for every r such that 0 < r there exists s such that 0 < s and for all x1 , x2 such that x1 ∈ X and x2 ∈ X and kx1 − x2 k < s holds |fx1 − fx2 | < r. The following propositions are true: (1) If f is uniformly continuous on X and X1 ⊆ X, then f is uniformly continuous ...