PPT
... Thus, x1 15 By doubling bound, x1 16 But x1 ≠ 16 since there is only one way to make 16 in 4 stages and it does not make 14 along the way. Thus, x1 = 15 and M(15)=4 ...
... Thus, x1 15 By doubling bound, x1 16 But x1 ≠ 16 since there is only one way to make 16 in 4 stages and it does not make 14 along the way. Thus, x1 = 15 and M(15)=4 ...
Full text
... This shows that this 'terminal-edges-except-for-the-rightmost-edge! condition precisely yields the set A(T) where T is a composition. Next we have that A*(T) consists of all trees such that all ^dges except the leftmost up from a vertex are terminal. From here it is not hard to see that A (T) is aga ...
... This shows that this 'terminal-edges-except-for-the-rightmost-edge! condition precisely yields the set A(T) where T is a composition. Next we have that A*(T) consists of all trees such that all ^dges except the leftmost up from a vertex are terminal. From here it is not hard to see that A (T) is aga ...
Integers - Duplin County Schools
... • The sum of two positive integers is always positive. • The sum of two negative integers is always negative. • When you add a positive and negative integer, you are really subtracting. Then, you give the answer the sign of the greater absolute value. ...
... • The sum of two positive integers is always positive. • The sum of two negative integers is always negative. • When you add a positive and negative integer, you are really subtracting. Then, you give the answer the sign of the greater absolute value. ...
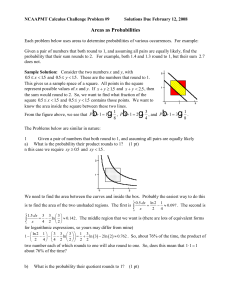
NCAAPMT Calculus Challenge Problem #9 Solutions Due February
... of 1 and the red begin with 5. The areas of the two triangles below y = x are the same. If the ratio is less than one, then the first non-zero digits are uniformly distributed. However, if the ratio is larger than one, things get more interesting. Notice how much larger the region between y = x and ...
... of 1 and the red begin with 5. The areas of the two triangles below y = x are the same. If the ratio is less than one, then the first non-zero digits are uniformly distributed. However, if the ratio is larger than one, things get more interesting. Notice how much larger the region between y = x and ...
Mathematical Ideas - Folsom Lake College
... Reading from right to left, the rods have values of 1, 10, 100, 1000, and so on. The bead above the bar has five times the value of those below. Beads moved towards the bar are in “active” position. ...
... Reading from right to left, the rods have values of 1, 10, 100, 1000, and so on. The bead above the bar has five times the value of those below. Beads moved towards the bar are in “active” position. ...
Plan - Activities for the kids
... 3a) understand addition and use related vocabulary; recognise that addition can be done in any order; understand subtraction as both ‘take away’ and ‘difference’ and use the related vocabulary 3c) develop rapid recall of number facts: know addition and subtraction facts to 10 and then use these to d ...
... 3a) understand addition and use related vocabulary; recognise that addition can be done in any order; understand subtraction as both ‘take away’ and ‘difference’ and use the related vocabulary 3c) develop rapid recall of number facts: know addition and subtraction facts to 10 and then use these to d ...
Std 02 Exponent Notes
... For any rational number a (except a = 0), and for all whole numbers m and n, n _________ a When dividing numbers with the same base, you _______________ the exponents. ...
... For any rational number a (except a = 0), and for all whole numbers m and n, n _________ a When dividing numbers with the same base, you _______________ the exponents. ...
Jugendtraum of a Mathematician
... complex numbers always has a solution in complex numbers (Gauss), and (ii) closedness under taking limits where distance between two complex numbers z1 , z2 is measured by the absolute value |z1 − z2 |. Furthermore, every proof of (i) essentially uses a property, called the conformality of the produ ...
... complex numbers always has a solution in complex numbers (Gauss), and (ii) closedness under taking limits where distance between two complex numbers z1 , z2 is measured by the absolute value |z1 − z2 |. Furthermore, every proof of (i) essentially uses a property, called the conformality of the produ ...
Lesson 1 Homework 5
... Lesson 1: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org ...
... Lesson 1: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.