Whole School Written Calculation Policy
... - = signs and missing numbers Continue using a range of equations as in Level 1 but with appropriate numbers. Extend to 14 + 5 = 20 - Find a small difference by counting up ...
... - = signs and missing numbers Continue using a range of equations as in Level 1 but with appropriate numbers. Extend to 14 + 5 = 20 - Find a small difference by counting up ...
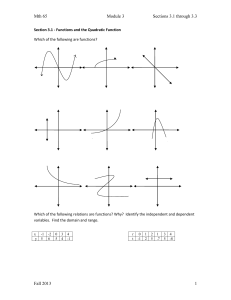
Mth 65 Module 3 Sections 3.1 through 3.3 Section 3.1
... The function above is called a _______________________________function. The shape of the graph is called a ___________________________. Each parabola has a _______________(maximum or minimum) and an axis of symmetry (always a ______________________ line which passes through the vertex). State the ve ...
... The function above is called a _______________________________function. The shape of the graph is called a ___________________________. Each parabola has a _______________(maximum or minimum) and an axis of symmetry (always a ______________________ line which passes through the vertex). State the ve ...
Chapter 2 Lesson 1: Rational Numbers
... cream. A dish with two scoops can have any two flavors, including the same flavor twice. How many different double-scoop combinations are possible? ...
... cream. A dish with two scoops can have any two flavors, including the same flavor twice. How many different double-scoop combinations are possible? ...
45rd IMO 2004 Problem 1. Let ABC be an acute
... Problem 3. Define a ”hook” to be a figure made up of six unit squares as shown below in the picture, or any of the figures obtained by applying rotations and reflections to this figure. ...
... Problem 3. Define a ”hook” to be a figure made up of six unit squares as shown below in the picture, or any of the figures obtained by applying rotations and reflections to this figure. ...
Click here
... 3.11 Suppose x ∈ R∗ has finite order, say, xn = 1. Notice then that |xn | = |x|n = 1, and that the only numbers that could qualify are x = ±1. Indeed, these have finite order of 1 and 2. 3.28 Since H contains 18 and 30, it must contain 30 − 18 = 12. Since H contains 30 and 40, it must contain 40 − 3 ...
... 3.11 Suppose x ∈ R∗ has finite order, say, xn = 1. Notice then that |xn | = |x|n = 1, and that the only numbers that could qualify are x = ±1. Indeed, these have finite order of 1 and 2. 3.28 Since H contains 18 and 30, it must contain 30 − 18 = 12. Since H contains 30 and 40, it must contain 40 − 3 ...
To write a number in scientific notation
... The first number 1.23 is called the coefficient. It must be greater than or equal to 1 and less than 10. The second number is called the base . It must always be 10 in scientific notation. The base number 10 is always written in exponent form. In the number 1.23 x 1011 the number 11 is referred to a ...
... The first number 1.23 is called the coefficient. It must be greater than or equal to 1 and less than 10. The second number is called the base . It must always be 10 in scientific notation. The base number 10 is always written in exponent form. In the number 1.23 x 1011 the number 11 is referred to a ...
unit 2 - Algebra 1 -
... HINTS to remember which inequality is which: 1) The arrow always points to the smaller number. 2) The “alligator” eats the bigger number. OPPOSITE – the opposite of a number is the same number with the other sign (positive or negative) Examples of opposites include: 1) –4 and 4 2) 19 and –19 3) ...
... HINTS to remember which inequality is which: 1) The arrow always points to the smaller number. 2) The “alligator” eats the bigger number. OPPOSITE – the opposite of a number is the same number with the other sign (positive or negative) Examples of opposites include: 1) –4 and 4 2) 19 and –19 3) ...
Translating Word Problems
... Note: Feel free to add more words to these lists as you find them. This is only a list of the more common words and is not meant to be complete. Steps for Translation Word Problems I. Find all the numbers and variables (unknowns) in the problem, write them down above (or below) the word. (If it is a ...
... Note: Feel free to add more words to these lists as you find them. This is only a list of the more common words and is not meant to be complete. Steps for Translation Word Problems I. Find all the numbers and variables (unknowns) in the problem, write them down above (or below) the word. (If it is a ...
Rational Approximations of Irrational Numbers
... paradoxical to students. First, 7 (or any irrational number) is an exact value, while 2.64575 is an approximation, no matter how many decimal places it is extended. Secondly, there is a precise point on the number line where 7 is located even though it is difficult to locate. Students need to unders ...
... paradoxical to students. First, 7 (or any irrational number) is an exact value, while 2.64575 is an approximation, no matter how many decimal places it is extended. Secondly, there is a precise point on the number line where 7 is located even though it is difficult to locate. Students need to unders ...
Number Representation
... • First, what is (-57ten) in binary in 8 bits? 1. 00111001 (57ten in binary) 2. 11000110 (invert) 3. 11000111 (add 1) ...
... • First, what is (-57ten) in binary in 8 bits? 1. 00111001 (57ten in binary) 2. 11000110 (invert) 3. 11000111 (add 1) ...
Big Apple Academy Mathematics Department Grade 2 → 3 Summer
... It is important that you keep practicing your mathematical Knowledge over the summer to be ready for 3rd grade. In this Package you will find a calendar of activities for the month of July and August. What should you do? ...
... It is important that you keep practicing your mathematical Knowledge over the summer to be ready for 3rd grade. In this Package you will find a calendar of activities for the month of July and August. What should you do? ...
- Canyon Grove Distance Education
... 4.OA.5 .b □ I can use the Commutative property of multiplication (I know that if 6 x 4 = 24, then 4 x 6 = 24). ...
... 4.OA.5 .b □ I can use the Commutative property of multiplication (I know that if 6 x 4 = 24, then 4 x 6 = 24). ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.