Views of Pi: definition and computation
... The number π has been a fascinating object for mathematicians for many centuries. It is both a very concrete number and an abstract one. It is concrete because it is a simple ratio between either the respective surfaces of a circle and a square or between the perimeter of a circle and its diameter. ...
... The number π has been a fascinating object for mathematicians for many centuries. It is both a very concrete number and an abstract one. It is concrete because it is a simple ratio between either the respective surfaces of a circle and a square or between the perimeter of a circle and its diameter. ...
KENO, KENO BONUS, KENO PATTERN PLAY
... limited to $2,000,000 less the aggregate of all prizes in such draw of $1,000 or less. For draws which include tickets with Keno Doubler, the aggregate amount that may be won in any given draw by all ticket holders whose unadjusted prizes exceeds $1,000 shall be limited to $4,000,000 less the aggreg ...
... limited to $2,000,000 less the aggregate of all prizes in such draw of $1,000 or less. For draws which include tickets with Keno Doubler, the aggregate amount that may be won in any given draw by all ticket holders whose unadjusted prizes exceeds $1,000 shall be limited to $4,000,000 less the aggreg ...
Complex Numbers
... 4. angle( -given the angle that the segment from the point (0, 0) to the point (a, b) makes with the positive end of the x-axis. The angle is also called the argument of the complex number. Exercise 16. Find the argument of the complex numbers a) 3 + 4i b) -3 + 3i 3 -i (set the calculator in degre ...
... 4. angle( -given the angle that the segment from the point (0, 0) to the point (a, b) makes with the positive end of the x-axis. The angle is also called the argument of the complex number. Exercise 16. Find the argument of the complex numbers a) 3 + 4i b) -3 + 3i 3 -i (set the calculator in degre ...
Basic Combinatorics - Math - The University of Tennessee, Knoxville
... this notation, one would write M = {13 , 24 , 31 }. The list of objects belonging to a multiset is always enclosed by a pair of curly brackets. The cardinality (i.e., number of elements) of a multiset takes account of repetitions. So, for example, the multiset M has cardinality 8. A set is simply a ...
... this notation, one would write M = {13 , 24 , 31 }. The list of objects belonging to a multiset is always enclosed by a pair of curly brackets. The cardinality (i.e., number of elements) of a multiset takes account of repetitions. So, for example, the multiset M has cardinality 8. A set is simply a ...
2015 Mathematics Contests – The Australian Scene Part 1
... Challenge continuing to grow, helped by the gathering momentum of the new Middle Primary Division, which began in 2014. The Enrichment stage, containing course work, allows students to broaden their knowledge base in the areas of mathematics associated with the Olympiad programs and more advanced pr ...
... Challenge continuing to grow, helped by the gathering momentum of the new Middle Primary Division, which began in 2014. The Enrichment stage, containing course work, allows students to broaden their knowledge base in the areas of mathematics associated with the Olympiad programs and more advanced pr ...
9.8 Printing with Field Widths and Precision
... printf( "Enter seven integers: " ); scanf( "%d%i%i%i%o%u%x", &a, &b, &c, &d, &e, &f, &g ); printf( "The input displayed as decimal integers is:\n" ); printf( "%d %d %d %d %d %d %d\n", a, b, c, d, e, f, g ); return 0; /* indicates successful termination */ ...
... printf( "Enter seven integers: " ); scanf( "%d%i%i%i%o%u%x", &a, &b, &c, &d, &e, &f, &g ); printf( "The input displayed as decimal integers is:\n" ); printf( "%d %d %d %d %d %d %d\n", a, b, c, d, e, f, g ); return 0; /* indicates successful termination */ ...
FERMAT`S LITTLE THEOREM 1. Introduction When we compute the
... m is prime. But 3m−1 ≡ 76861 6≡ 1 mod m, so a = 3 would violate Fermat’s little theorem if m were prime, so it can’t be prime. The number 80581 must be composite. These examples illustrate a point that is at first hard to believe: proving a number is composite and factoring a number in a nontrivial ...
... m is prime. But 3m−1 ≡ 76861 6≡ 1 mod m, so a = 3 would violate Fermat’s little theorem if m were prime, so it can’t be prime. The number 80581 must be composite. These examples illustrate a point that is at first hard to believe: proving a number is composite and factoring a number in a nontrivial ...
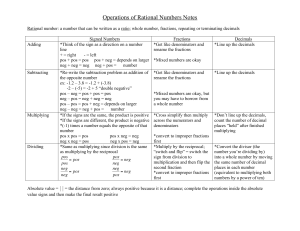
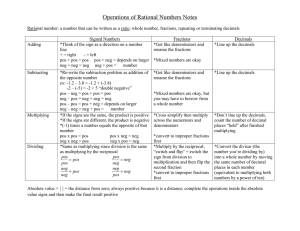
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.