Problem Set 3
... MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 3 Unlike the previous problem set, in this one you will need to prove your claims rigorously. 1. (a) Prove Bernoulli’s inequality: (1 + x)n ≥ 1 + nx for every real number x ≥ −1 and every n ∈ N. (b) Define the sequence (an )n∈N and (bn )n∈N ...
... MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 3 Unlike the previous problem set, in this one you will need to prove your claims rigorously. 1. (a) Prove Bernoulli’s inequality: (1 + x)n ≥ 1 + nx for every real number x ≥ −1 and every n ∈ N. (b) Define the sequence (an )n∈N and (bn )n∈N ...
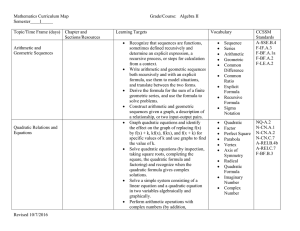
Algebra I Study Guide for End of Course Test
... REMEMBER: x 1 , a a . Anything to the 0 power, is always 1. Anything to the 1st power is always itself. Commutative Property: communicate your order at the Sonic, therefore commutative is to change the order of the operation. a+b=b+a Example: 1 + 2 = 2 + 1 (you still get the same answer) Associa ...
... REMEMBER: x 1 , a a . Anything to the 0 power, is always 1. Anything to the 1st power is always itself. Commutative Property: communicate your order at the Sonic, therefore commutative is to change the order of the operation. a+b=b+a Example: 1 + 2 = 2 + 1 (you still get the same answer) Associa ...
SAR Worksheet – Rounding 1000′s - Slide-A
... office supplies to his co-worker. He dropped 1,829 large paper clips and 1,212 small paper clips. Rounding to the nearest thousand, approximately how many paper clips did John drop? ...
... office supplies to his co-worker. He dropped 1,829 large paper clips and 1,212 small paper clips. Rounding to the nearest thousand, approximately how many paper clips did John drop? ...
Chapter 4 Complex Numbers
... Complex numbers can be represented as points on a grid that appears identical to the Cartesian co-ordinate grid (the xy-plane) except that the horizontal axis is called the real axis, and the vertical axis is interpreted as the imaginary axis. The axes are labeled respectively as Re{z} and Im{z}. Fr ...
... Complex numbers can be represented as points on a grid that appears identical to the Cartesian co-ordinate grid (the xy-plane) except that the horizontal axis is called the real axis, and the vertical axis is interpreted as the imaginary axis. The axes are labeled respectively as Re{z} and Im{z}. Fr ...
Compound Inequalities
... When solving equations, we follow the rule, “What you do to one side, you must do to the other.” The same applies to solving inequalities. Ex: ...
... When solving equations, we follow the rule, “What you do to one side, you must do to the other.” The same applies to solving inequalities. Ex: ...
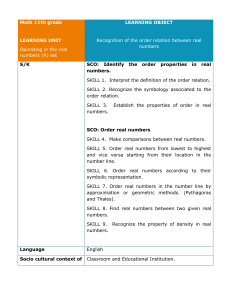
High School Math 2 Unit 1: Extending the Number System
... N.RN.3 Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a nonzero rational number and an irrational number is irrational. Perform arithmetic operations on polynomials. A.APR.1 Und ...
... N.RN.3 Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a nonzero rational number and an irrational number is irrational. Perform arithmetic operations on polynomials. A.APR.1 Und ...
Best Student Solutions
... 5. Note that the middle barrel is not used in any of the sides, so we place 9 there. The remaining barrels add up to 36, but note that the barrels on the vertices are added along two sides. We place 0 (the unmarked barrel), 1, and 2 along these sides, giving us a total of 39, divided equally among t ...
... 5. Note that the middle barrel is not used in any of the sides, so we place 9 there. The remaining barrels add up to 36, but note that the barrels on the vertices are added along two sides. We place 0 (the unmarked barrel), 1, and 2 along these sides, giving us a total of 39, divided equally among t ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.