polynomial function
... A real number a is a zero of a function y = f (x) if and only if f (a) = 0. Real Zeros of Polynomial Functions If y = f (x) is a polynomial function and a is a real number then the following statements are equivalent. 1. (a, 0) is a zero of f. 2. x = a is a solution of the polynomial equation f (x) ...
... A real number a is a zero of a function y = f (x) if and only if f (a) = 0. Real Zeros of Polynomial Functions If y = f (x) is a polynomial function and a is a real number then the following statements are equivalent. 1. (a, 0) is a zero of f. 2. x = a is a solution of the polynomial equation f (x) ...
Advanced Algorithms
... • We maintain a parallel array s[i, j] in which we store the value of k providing the optimal split .Leave a split marker indicating where the best split is (i.e. the value of k leading to minimum values of m[i, j]).. • If s[i, j] = k, the best way to multiply the sub-chain Ai…j is to first multiply ...
... • We maintain a parallel array s[i, j] in which we store the value of k providing the optimal split .Leave a split marker indicating where the best split is (i.e. the value of k leading to minimum values of m[i, j]).. • If s[i, j] = k, the best way to multiply the sub-chain Ai…j is to first multiply ...
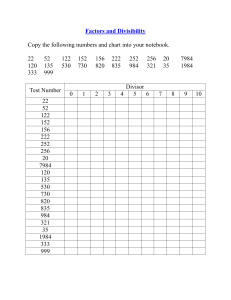
Factors and Divisibility
... If the last two digits are divisible by 4 then the entire number is divisible by 4. For example, 8316. Since the last 2 digits are 16 and 16 is divisible by 4, then 8316 is divisible by 4. ...
... If the last two digits are divisible by 4 then the entire number is divisible by 4. For example, 8316. Since the last 2 digits are 16 and 16 is divisible by 4, then 8316 is divisible by 4. ...
Sample 11+ Assessment Test — Maths 1
... What is the total volume of these two cuboids combined? A 240 cm³ C 120 cm³ E 30 cm³ D 60 cm³ B 480 cm³ ...
... What is the total volume of these two cuboids combined? A 240 cm³ C 120 cm³ E 30 cm³ D 60 cm³ B 480 cm³ ...
lect22
... processing to do. Now our general case needs to bring us closer to the base case situation. That is, the length of the array to be processed decreases by 1 with each recursive call. By printing one element in the general case, and also processing the smaller array, we will eventually reach the situa ...
... processing to do. Now our general case needs to bring us closer to the base case situation. That is, the length of the array to be processed decreases by 1 with each recursive call. By printing one element in the general case, and also processing the smaller array, we will eventually reach the situa ...
Name - Wantagh School
... The “i” tells you that it is not only a point, but a vector. You must draw an arrow from the origin (0, 0) to the point that you graphed. ...
... The “i” tells you that it is not only a point, but a vector. You must draw an arrow from the origin (0, 0) to the point that you graphed. ...
Examples of Functions
... are real numbers. A linear polynomial is a mathematical creature just like natural numbers, rational numbers, irrational numbers, matrices, and vectors are mathematical creatures. There is no equation involved. The concept of solving a linear polynomial is meaningless. The arithmetic-like concepts o ...
... are real numbers. A linear polynomial is a mathematical creature just like natural numbers, rational numbers, irrational numbers, matrices, and vectors are mathematical creatures. There is no equation involved. The concept of solving a linear polynomial is meaningless. The arithmetic-like concepts o ...
Tau Numbers: A Partial Proof of a Conjecture and Other Results
... Note that since the set A introduced in the proof of Theorem 25 contains many elements other than the primes, even if either the weak or the strong Goldbach conjectures fail to hold, it is still very likely that all integers can be expressed as the sum of six or fewer tau numbers. We make the follow ...
... Note that since the set A introduced in the proof of Theorem 25 contains many elements other than the primes, even if either the weak or the strong Goldbach conjectures fail to hold, it is still very likely that all integers can be expressed as the sum of six or fewer tau numbers. We make the follow ...
Document
... we are going to define a few “math words” Often, the instructions for homework problems are given, but since the student does not know what the “math words” mean, the instructions are misunderstood or ignored. The words we need to know are defined on the next two slides. Take a moment to write the w ...
... we are going to define a few “math words” Often, the instructions for homework problems are given, but since the student does not know what the “math words” mean, the instructions are misunderstood or ignored. The words we need to know are defined on the next two slides. Take a moment to write the w ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.