COMP4690 Tutorial
... DES works on bits DES works by encrypting groups of 64 bits, which is the same as 16 hexadecimal numbers DES uses keys which are also apparently 64 bits long. However, every 8th key bit is ignored in the DES algorithm, so the effective key size is 56 bits. If the length of the message to be ...
... DES works on bits DES works by encrypting groups of 64 bits, which is the same as 16 hexadecimal numbers DES uses keys which are also apparently 64 bits long. However, every 8th key bit is ignored in the DES algorithm, so the effective key size is 56 bits. If the length of the message to be ...
Solving Linear Inequalities in One Variable
... 3. Solve an application involving a linear inequality in one variable ...
... 3. Solve an application involving a linear inequality in one variable ...
5-CON TRIANGLES - Antonella Perucca
... triple is m2 and we only need to ensure m2 < 1+m; the second triple is obtained from the first by scaling with m. So we have two triangles: They are clearly similar and exactly two of the three side lengths coincide.).√ Some references work with m−1 < 1 instead, which leads to the inequalities 5−1 ...
... triple is m2 and we only need to ensure m2 < 1+m; the second triple is obtained from the first by scaling with m. So we have two triangles: They are clearly similar and exactly two of the three side lengths coincide.).√ Some references work with m−1 < 1 instead, which leads to the inequalities 5−1 ...
Fermat`s Little Theorem and Chinese Remainder Theorem Solutions
... Therefore if (m, n) is a solution with n ≥ 2 so that 4|2n , then 4 must divide 3m −1 = 2n and the equation above indicates m must be even. This allows us to factor: (3m/2 + 1)(3m/2 − 1) = 2n . Thus: a) (3m/2 + 1) and (3m/2 − 1) are both powers of 2 b) (3m/2 + 1) − (3m/2 − 1) = 2 What powers of 2 hav ...
... Therefore if (m, n) is a solution with n ≥ 2 so that 4|2n , then 4 must divide 3m −1 = 2n and the equation above indicates m must be even. This allows us to factor: (3m/2 + 1)(3m/2 − 1) = 2n . Thus: a) (3m/2 + 1) and (3m/2 − 1) are both powers of 2 b) (3m/2 + 1) − (3m/2 − 1) = 2 What powers of 2 hav ...
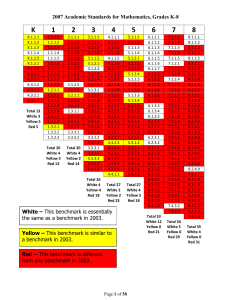
Standards with notes regarding 2003 Standards
... For example: A cylinder can be used to model a can of soup. objects. Another example: Find as many rectangles as you can in your classroom. Record the rectangles you found by making drawings. ...
... For example: A cylinder can be used to model a can of soup. objects. Another example: Find as many rectangles as you can in your classroom. Record the rectangles you found by making drawings. ...
Full text
... not divisible hyp is 2*13*24*3... rSr~l, where % is the number of I'S in the base p expansion of n. Proof: First, we note that the maximum exists. It is well known that rx
... not divisible hyp is 2*13*24*3... rSr~l, where % is the number of I'S in the base p expansion of n. Proof: First, we note that the maximum exists. It is well known that rx
1, so r < p +1. By Kummer's Theorem for Generalized Binomial Coefficients, /?|[£] g if ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.