Sequences
... To write a rule, look for the pattern between each number, subtraction, addition, or multiplication. Check the next several terms to see if it holds true. Let’s try another one. ...
... To write a rule, look for the pattern between each number, subtraction, addition, or multiplication. Check the next several terms to see if it holds true. Let’s try another one. ...
1. Complex Numbers and the Complex Exponential
... The set of all complex numbers (conventionally denoted by a fancy letter C: C, or C, or C) is the set of everything that can be written in the form x + yi, where x and y are real numbers. Addition and multiplication are performed as they would be for polynomials in the character “i” with the underst ...
... The set of all complex numbers (conventionally denoted by a fancy letter C: C, or C, or C) is the set of everything that can be written in the form x + yi, where x and y are real numbers. Addition and multiplication are performed as they would be for polynomials in the character “i” with the underst ...
Part 1 - CSUN.edu
... We have a good idea what finite sets are. In a finite set we can list all elements explicitly. However, infinite sets can be different. We know the infinite set of positive integers and for this set we can also list the elements, but we will never be able to finish the list. Infinite sets of this ty ...
... We have a good idea what finite sets are. In a finite set we can list all elements explicitly. However, infinite sets can be different. We know the infinite set of positive integers and for this set we can also list the elements, but we will never be able to finish the list. Infinite sets of this ty ...
1 Sets, functions and counting
... that f (a) = b. In particular we can define a function from B to A by associating to each b ∈ B the unique a ∈ A satisfying b = f (a). This is called the inverse function of f and denoted by f −1 : B → A. Symbolically, f −1 (b) = a iff f (a) = b. Note that the inverse function is also a bijective ma ...
... that f (a) = b. In particular we can define a function from B to A by associating to each b ∈ B the unique a ∈ A satisfying b = f (a). This is called the inverse function of f and denoted by f −1 : B → A. Symbolically, f −1 (b) = a iff f (a) = b. Note that the inverse function is also a bijective ma ...
1 - GEOCITIES.ws
... 30. 25 = 4! + 1. This is the only solution of (n-1)! + 1 = nk. 31. Fermat asserted correctly, without proving, that 52 = 25 = 33 – 2 is the only square that is 2 less than a cube. 32. 3x + 1 Problem: This problem starts with any number, divides it by 2 if it is even, and multiplies it by 3 and adds ...
... 30. 25 = 4! + 1. This is the only solution of (n-1)! + 1 = nk. 31. Fermat asserted correctly, without proving, that 52 = 25 = 33 – 2 is the only square that is 2 less than a cube. 32. 3x + 1 Problem: This problem starts with any number, divides it by 2 if it is even, and multiplies it by 3 and adds ...
![arXiv:1003.5939v1 [math.CO] 30 Mar 2010](http://s1.studyres.com/store/data/016290525_1-37241e0159a202e5bf035fd4e5a48270-300x300.png)
Week 2 - NUI Galway
... 1. The identity function f, defined by the rule f(x) = x, has R as its domain and codomain. Its range is also R. More precisely, every x ∈ R occurs exactly once as a value for f (of x itself). 2. The square function f(x) = x2 has R as its domain and codomain. Its range, however is [0, ∞), as x2 > 0 ...
... 1. The identity function f, defined by the rule f(x) = x, has R as its domain and codomain. Its range is also R. More precisely, every x ∈ R occurs exactly once as a value for f (of x itself). 2. The square function f(x) = x2 has R as its domain and codomain. Its range, however is [0, ∞), as x2 > 0 ...
Full text
... For larger values of m9 it is convenient to use recursion formulas with positive terms only 9 which will be connected with a closer investigation of irregular permutations. If we start from one of the um permutations belonging to U(m9 0)s say a9 and if we delete 7??+ 1 in a, the remaining permutatio ...
... For larger values of m9 it is convenient to use recursion formulas with positive terms only 9 which will be connected with a closer investigation of irregular permutations. If we start from one of the um permutations belonging to U(m9 0)s say a9 and if we delete 7??+ 1 in a, the remaining permutatio ...
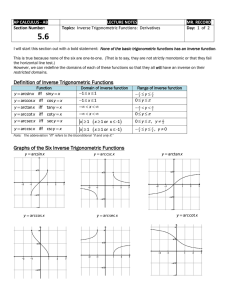
5.6: Inverse Trigonometric Functions: Differentiation
... LECTURE NOTES Topics: Inverse Trigonometric Functions: Derivatives - Inverse Trig Function Analyisis ...
... LECTURE NOTES Topics: Inverse Trigonometric Functions: Derivatives - Inverse Trig Function Analyisis ...
Gamma Function for Different Negative Numbers
... The behavior for negative n is more intricate. Euler's integral does not converge for n ≤ 0, but the function it defines in the positive complex half-plane has a unique analytic continuation to the negative half-plane. The gamma function is nonzero everywhere along the real line, although it comes a ...
... The behavior for negative n is more intricate. Euler's integral does not converge for n ≤ 0, but the function it defines in the positive complex half-plane has a unique analytic continuation to the negative half-plane. The gamma function is nonzero everywhere along the real line, although it comes a ...
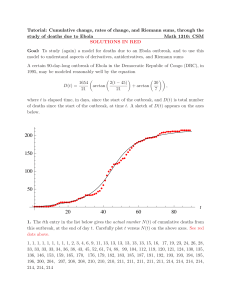
The Accumulation Function
... At what time during the first 9 seconds does s have its largest value? Approximately when is the acceleration zero? When is the particle moving toward the origin? Away from the origin? On which side of the origin does the particle lie at time t = 9? ...
... At what time during the first 9 seconds does s have its largest value? Approximately when is the acceleration zero? When is the particle moving toward the origin? Away from the origin? On which side of the origin does the particle lie at time t = 9? ...