6. Cardinality And The Strange Nature Of Infinity
... addition, if you are thinking “Of course they are incorrect. Each of these sets is infinite, so their cardinality is the same.” then you are also wrong. In fact, it turns out that ` = ] = _ < \ ! There are also infinite sets which are much bigger than \ . For example, the set of real valued function ...
... addition, if you are thinking “Of course they are incorrect. Each of these sets is infinite, so their cardinality is the same.” then you are also wrong. In fact, it turns out that ` = ] = _ < \ ! There are also infinite sets which are much bigger than \ . For example, the set of real valued function ...
A Geometric Proof that e is Irrational and a New
... q q for all p and q with q ≥ q(ε ) . This follows easily from the continued fraction expansion of e. (See, for example, [23]. For sharper inequalities than (13), see [3, Corollary 11.1], [4], [7], [10, pp. 112-113], and especially the elegant [26].) Presumably, (13) is usually stronger than (4). We ...
... q q for all p and q with q ≥ q(ε ) . This follows easily from the continued fraction expansion of e. (See, for example, [23]. For sharper inequalities than (13), see [3, Corollary 11.1], [4], [7], [10, pp. 112-113], and especially the elegant [26].) Presumably, (13) is usually stronger than (4). We ...
x - Coweta County Schools
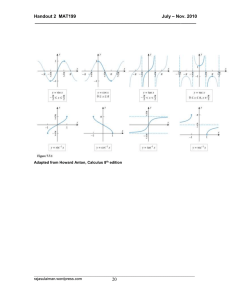
... Sandwich Theorem Revisited Infinite Limits as x→a End Behavior Models Seeing Limits as x→±∞ ...
... Sandwich Theorem Revisited Infinite Limits as x→a End Behavior Models Seeing Limits as x→±∞ ...
On the representation of an even perfect number as the sum of a
... where p and (2p − 1) are both primes. Concerning the odd perfect numbers, even if they were studied by several mathematicians, we don’t know up to now if there is anyone. The conjecture of odd perfect numbers states that such numbers do not exist (see, e.g., [2, 4]). This conjecture is probably the ...
... where p and (2p − 1) are both primes. Concerning the odd perfect numbers, even if they were studied by several mathematicians, we don’t know up to now if there is anyone. The conjecture of odd perfect numbers states that such numbers do not exist (see, e.g., [2, 4]). This conjecture is probably the ...
Math Cram Kit File
... LINEAR INEQUALITY An inequality with a degree of 1 18 < ---5x --- 7 25 < ---5x 5>x ...
... LINEAR INEQUALITY An inequality with a degree of 1 18 < ---5x --- 7 25 < ---5x 5>x ...
Waring`s problem, taxicab numbers, and other sums of powers
... π 2 n. But this method does not take into account purely number-theoretic considerations such as modular arithmetic; nor does it take into account that most k-tuples are counted “more than once” in Rk (n) due to the inherent symmetry of the problem. For sums of two squares, we actually have the foll ...
... π 2 n. But this method does not take into account purely number-theoretic considerations such as modular arithmetic; nor does it take into account that most k-tuples are counted “more than once” in Rk (n) due to the inherent symmetry of the problem. For sums of two squares, we actually have the foll ...
Full text
... (see [7]). Each multiplicative function is completely determined by its generating series (at all primes/?). It is easy to see that generating series can also be used in the context of quasi-multiplicative functions. The Dirichlet convolution f*g of two arithmetic functions/and g is defined by ...
... (see [7]). Each multiplicative function is completely determined by its generating series (at all primes/?). It is easy to see that generating series can also be used in the context of quasi-multiplicative functions. The Dirichlet convolution f*g of two arithmetic functions/and g is defined by ...
Lecture 22 - Duke Computer Science
... if when P is executed on an ideal computer, it outputs a sequence of symbols such that - The kth symbol that it outputs is sk - For every k, P eventually outputs the kth symbol. I.e., the delay between symbol k and symbol k+1 is not infinite ...
... if when P is executed on an ideal computer, it outputs a sequence of symbols such that - The kth symbol that it outputs is sk - For every k, P eventually outputs the kth symbol. I.e., the delay between symbol k and symbol k+1 is not infinite ...