1 + - Mathematical Association of America
... g(x) > 0 for all x ∈ (l, r ). (Of course, a similar statement holds if both inequalities are reversed.) Now, by differentiating and using a little algebra, we find that ...
... g(x) > 0 for all x ∈ (l, r ). (Of course, a similar statement holds if both inequalities are reversed.) Now, by differentiating and using a little algebra, we find that ...
Applications of the Complex Roots of Unity - Rose
... Consider the following table of factored Mersenne numbers. Notice that 3 appears as a factor in every second Mersenne number, 5 appears as a factor in every fourth Mersenne number, and 7 appears as a factor in every third Mersenne number. The prime 2 does not appear since all Mersenne numbers are od ...
... Consider the following table of factored Mersenne numbers. Notice that 3 appears as a factor in every second Mersenne number, 5 appears as a factor in every fourth Mersenne number, and 7 appears as a factor in every third Mersenne number. The prime 2 does not appear since all Mersenne numbers are od ...
Absolute polynomial factorization in two variables and the knapsack
... total degree n. Consider Q(x, y, λ) = P (x + λy, y). Then for P almost all specializations (x0 , λ0 ) of (x, λ), the sums Q i∈J bi (x0 ), for J in {1, · · · , n}, vanish if and only if j∈J (Y − ϕj (X)) is a polynomial factor of P . This theorem gives rise to an algorithm modulo the following combina ...
... total degree n. Consider Q(x, y, λ) = P (x + λy, y). Then for P almost all specializations (x0 , λ0 ) of (x, λ), the sums Q i∈J bi (x0 ), for J in {1, · · · , n}, vanish if and only if j∈J (Y − ϕj (X)) is a polynomial factor of P . This theorem gives rise to an algorithm modulo the following combina ...
Maximum Likelihood Estimator
... The distributions of the estimators become more and more concentrated near the true value of the parameter being estimated. ...
... The distributions of the estimators become more and more concentrated near the true value of the parameter being estimated. ...
12-1 Notes 9/6/16 (Introduction to Sequences)
... Example 5: Iteration of Fractals Find the number of triangles in the 7th and 8th iterations of the Sierpinski triangle. By removing the center of each triangle, each iteration turns every triangle into 3 smaller triangles. So the number of triangles triples with each iteration. The number of triangl ...
... Example 5: Iteration of Fractals Find the number of triangles in the 7th and 8th iterations of the Sierpinski triangle. By removing the center of each triangle, each iteration turns every triangle into 3 smaller triangles. So the number of triangles triples with each iteration. The number of triangl ...
MATH 337 Cardinality
... So far, we have three types of cardinalities: finite, denumerable, uncountable. These cardinalities create different numbers: 0, 1, 2, 3, . . ., n , . . . , ℵ0 , c . The symbol ℵ0 represents the countably infinite cardinality of the natural numbers and is also called first infinite ordinal. The symb ...
... So far, we have three types of cardinalities: finite, denumerable, uncountable. These cardinalities create different numbers: 0, 1, 2, 3, . . ., n , . . . , ℵ0 , c . The symbol ℵ0 represents the countably infinite cardinality of the natural numbers and is also called first infinite ordinal. The symb ...
Sequences - Pearson Schools and FE Colleges
... Explain that a sequence is a set of numbers in a given order, but that often the order is given by a rule. Can you give me examples of other number sequences? (Answers could be: sequences following a simple rule such as square numbers; sequences following a more complex rule such as time of sunset e ...
... Explain that a sequence is a set of numbers in a given order, but that often the order is given by a rule. Can you give me examples of other number sequences? (Answers could be: sequences following a simple rule such as square numbers; sequences following a more complex rule such as time of sunset e ...
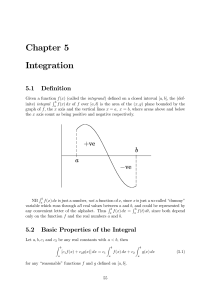
Chapter 5 Integration
... The rules (5.11) and (5.13) for change of variable in definite and indefinite integrals may be summarized as follows. ² In both cases express the original integrand in terms of the new variable and transform the differential via (5.12). ² In the indefinite case (5.13), reexpress the new indefinite i ...
... The rules (5.11) and (5.13) for change of variable in definite and indefinite integrals may be summarized as follows. ² In both cases express the original integrand in terms of the new variable and transform the differential via (5.12). ² In the indefinite case (5.13), reexpress the new indefinite i ...
Notes
... school). To compute a bit in the kth place after the binary point (corresponding to the value 2−k ), we see whether 2−k d is greater than the current remainder; if it is, then we set the bit to one and update the remainder. This algorithm is shown in Figure 1. At step k of long division, we have an ...
... school). To compute a bit in the kth place after the binary point (corresponding to the value 2−k ), we see whether 2−k d is greater than the current remainder; if it is, then we set the bit to one and update the remainder. This algorithm is shown in Figure 1. At step k of long division, we have an ...
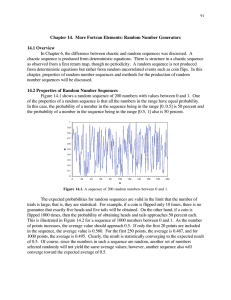
Chapter 14. More Fortran Elements: Random Number Generators
... sequences. That is, if the random number generator is given the same starting value (called the seed), then it will produce the same sequence every time. This behavior is known as a pseudorandom sequence, and it is useful for testing the Fortran code. The properties of a pseudo-random sequence are t ...
... sequences. That is, if the random number generator is given the same starting value (called the seed), then it will produce the same sequence every time. This behavior is known as a pseudorandom sequence, and it is useful for testing the Fortran code. The properties of a pseudo-random sequence are t ...