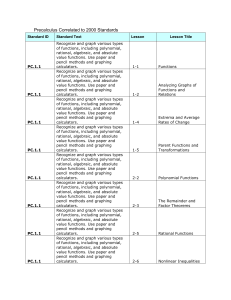
10 Sequences PowerPoint
... integers increase without bound – no matter how large an integer you can think of you can always add 1 to it to obtain an even larger integer. An alternative description of this idea is to say that the integers increase to infinity where infinity is represented by the symbol ∞ (negative infinity is ...
... integers increase without bound – no matter how large an integer you can think of you can always add 1 to it to obtain an even larger integer. An alternative description of this idea is to say that the integers increase to infinity where infinity is represented by the symbol ∞ (negative infinity is ...
5. p-adic Numbers 5.1. Motivating examples. We all know that √2 is
... For example, the usual absolute value |x| is a norm on the fields Q, R and C. We sometimes write this as |x|∞ by analogy with the p-adic norms introduced below. The trivial norm, defined by kxk = 1 for all nonzero x, is a norm on any field. Note that the multiplicativity and positivity always imply ...
... For example, the usual absolute value |x| is a norm on the fields Q, R and C. We sometimes write this as |x|∞ by analogy with the p-adic norms introduced below. The trivial norm, defined by kxk = 1 for all nonzero x, is a norm on any field. Note that the multiplicativity and positivity always imply ...
Summer Review Packet for Students Entering Calculus (all levels)
... 2. How many of that type of x do you have in the numerator? 3. How many of that type of x do you have in the denominator? 4. That ratio is your limit! 2x 5 4 x 2 lim x 3 5x x 2 ...
... 2. How many of that type of x do you have in the numerator? 3. How many of that type of x do you have in the denominator? 4. That ratio is your limit! 2x 5 4 x 2 lim x 3 5x x 2 ...
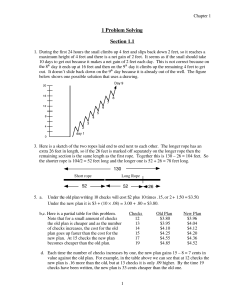
FOR STARTERS
... 1.4 Solving Multi-Step Equations To isolate the variable, simplify each side if applicable, and then undo the operations. ...
... 1.4 Solving Multi-Step Equations To isolate the variable, simplify each side if applicable, and then undo the operations. ...
Discrete mathematics and algebra
... where otherwise indicated. All rights reserved. No part of this work may be reproduced in any form, or by any means, without permission in writing from the publisher. We make every effort to contact copyright holders. If you think we have inadvertently used your copyright material, please let us kno ...
... where otherwise indicated. All rights reserved. No part of this work may be reproduced in any form, or by any means, without permission in writing from the publisher. We make every effort to contact copyright holders. If you think we have inadvertently used your copyright material, please let us kno ...
4.2.1 Adding and Subtracting Polynomials
... • When there are two or more variables in a polynomial, the terms are written in descending order alphabetically. For example, x2 + x + y2 + y + 12 is written in descending order alphabetically. • To add or subtract like terms containing a variable, use the Distributive Property to add or subtract t ...
... • When there are two or more variables in a polynomial, the terms are written in descending order alphabetically. For example, x2 + x + y2 + y + 12 is written in descending order alphabetically. • To add or subtract like terms containing a variable, use the Distributive Property to add or subtract t ...
One, two, skip a few
... moves required to move n disks from one peg to another. (“T" for Tower.) So far, we have T1 = 1, T2 = 3, and T3 = 7. There is an even smaller case we haven’t considered yet: T0 = 0, since it takes no moves to move no disks!1 Now that we’ve handled some small cases, let’s think big. How would we deal ...
... moves required to move n disks from one peg to another. (“T" for Tower.) So far, we have T1 = 1, T2 = 3, and T3 = 7. There is an even smaller case we haven’t considered yet: T0 = 0, since it takes no moves to move no disks!1 Now that we’ve handled some small cases, let’s think big. How would we deal ...
RATIONAL FUNCTIONS AND REAL SCHUBERT CALCULUS 1
... positive integers, such that an integer k appears ak times, the entries are strictly increasing in the columns and non-decreasing in the rows. The corresponding Kostka number Ka is the number of such SSYT. Schubert calculus interpretation of these numbers shows that Ka does not change if we permute ...
... positive integers, such that an integer k appears ak times, the entries are strictly increasing in the columns and non-decreasing in the rows. The corresponding Kostka number Ka is the number of such SSYT. Schubert calculus interpretation of these numbers shows that Ka does not change if we permute ...