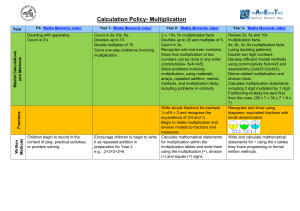
6th Grade
... 1. In the figure below angle m B= 45 ; A and D are right angles; mE = mF =135 . What is the area of the figure? ...
... 1. In the figure below angle m B= 45 ; A and D are right angles; mE = mF =135 . What is the area of the figure? ...
THE NUMBER FIELD SIEVE FOR INTEGERS OF LOW WEIGHT 1
... Notice that the weight of N does not appear in (2.3) but instead influences the bound on the size of the coefficients of f indirectly by imposing a lower bound on the size of the maximal gap in sequence (2.2). In the case that N is prime, it follows from a result in [4] that f is irreducible. In the ca ...
... Notice that the weight of N does not appear in (2.3) but instead influences the bound on the size of the coefficients of f indirectly by imposing a lower bound on the size of the maximal gap in sequence (2.2). In the case that N is prime, it follows from a result in [4] that f is irreducible. In the ca ...
SAT Practice Test #2 IMPORTANT REMINDERS
... the directions before question 16 on how to enter your answers in the grid. You may use any available space in your test booklet for scratch work. ...
... the directions before question 16 on how to enter your answers in the grid. You may use any available space in your test booklet for scratch work. ...
JHMCguide
... p1 , p 2 ,, p k are the different prime factors of n. Then, d(n), the number of divisors in n, is determined by d (n) (r1 1)( r2 1) (rk 1) Most mathematical theorems are written in this format. Its conciseness helps for reference. See if you can understand it. In plain language, this theor ...
... p1 , p 2 ,, p k are the different prime factors of n. Then, d(n), the number of divisors in n, is determined by d (n) (r1 1)( r2 1) (rk 1) Most mathematical theorems are written in this format. Its conciseness helps for reference. See if you can understand it. In plain language, this theor ...
hca04_0307
... Let P( x) an x n an 1 x n 1 a1 x a0 , where an 0, define a polynomial function w ith integer coefficients. If p / q is a rational number wri tten in lowest terms, and if p / q is a zero of P, then p is a factor of the constant term a0 , and q is a factor of the leading coefficient an ...
... Let P( x) an x n an 1 x n 1 a1 x a0 , where an 0, define a polynomial function w ith integer coefficients. If p / q is a rational number wri tten in lowest terms, and if p / q is a zero of P, then p is a factor of the constant term a0 , and q is a factor of the leading coefficient an ...
1-15 Final Review - Amundsen High School
... Adding numbers with the same sign Adding numbers with different signs Subtracting numbers Multiply/Dividing numbers with same sign Multiply/Divide numbers with different signs Order of Operations ...
... Adding numbers with the same sign Adding numbers with different signs Subtracting numbers Multiply/Dividing numbers with same sign Multiply/Divide numbers with different signs Order of Operations ...
![Maximum subsets of (0,1] with no solutions to x](http://s1.studyres.com/store/data/004884619_1-aef9649f88c5cc5f6ca0274124904717-300x300.png)
Maximum subsets of (0,1] with no solutions to x
... is S such that x + y = z. If k is a positive integer we say that a set S of real numbers is k-sum-free if there do not exist x, y, z in S such that x + y = kz (we require that not all x, y, and z be equal to each other to avoid a meaningless problem when k = 2). Let f (n, k) denote the maximum size ...
... is S such that x + y = z. If k is a positive integer we say that a set S of real numbers is k-sum-free if there do not exist x, y, z in S such that x + y = kz (we require that not all x, y, and z be equal to each other to avoid a meaningless problem when k = 2). Let f (n, k) denote the maximum size ...
Chapter 1.3
... Half-life Exponential functions can also model phenomena that produce decrease over time, such as happens with radioactive decay. The half-life of a radioactive substance is the amount of time it takes for half of the substance to change from its original radioactive state to a non-radioactive stat ...
... Half-life Exponential functions can also model phenomena that produce decrease over time, such as happens with radioactive decay. The half-life of a radioactive substance is the amount of time it takes for half of the substance to change from its original radioactive state to a non-radioactive stat ...
Elementary mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. The most basic topics in elementary mathematics are arithmetic and geometry. Beginning in the last decades of the 20th century, there has been an increased emphasis on problem solving. Elementary mathematics is used in everyday life in such activities as making change, cooking, buying and selling stock, and gambling. It is also an essential first step on the path to understanding science.In secondary school, the main topics in elementary mathematics are algebra and trigonometry. Calculus, even though it is often taught to advanced secondary school students, is usually considered college level mathematics.