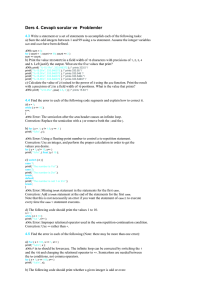
Example: Change 8/3 to a mixed number.
... To change an improper fraction to a mixed number, divide the numerator by the denominator. Example: Change 8/3 to a mixed number. Step 1: Divide the numerator by the denominator. (8 divided by 3= 2 and 2 out of 3 parts) Step 2: Write the remainder as a fraction. 2 2/3 The fraction 8/3 is the mixed n ...
... To change an improper fraction to a mixed number, divide the numerator by the denominator. Example: Change 8/3 to a mixed number. Step 1: Divide the numerator by the denominator. (8 divided by 3= 2 and 2 out of 3 parts) Step 2: Write the remainder as a fraction. 2 2/3 The fraction 8/3 is the mixed n ...
CSE 1400 Applied Discrete Mathematics Permutations
... set with cardinality |A| = n. There are n factorial different permutations of the elements in A. Figure 1 shows the 3! = 6 permutations of the elements in {0, 1, 2} written in cyclic notation. The permutations on {0, 1, 2, 3} can be defined recursively, that is, from the permutations on {0, 1, 2}. F ...
... set with cardinality |A| = n. There are n factorial different permutations of the elements in A. Figure 1 shows the 3! = 6 permutations of the elements in {0, 1, 2} written in cyclic notation. The permutations on {0, 1, 2, 3} can be defined recursively, that is, from the permutations on {0, 1, 2}. F ...
Chapter 4 The Group Zoo
... identity element 1̄: a · 1̄ = a. But not every a has an inverse! For an inverse ā−1 of ā to exist, we need aa−1 = 1 + zn, where z ∈ Z. Example 7. If n = 4, 2 cannot have an inverse, because 2 multiplied by any integer is even, and thus cannot be equal to 1 + 4z which is odd. To understand when an ...
... identity element 1̄: a · 1̄ = a. But not every a has an inverse! For an inverse ā−1 of ā to exist, we need aa−1 = 1 + zn, where z ∈ Z. Example 7. If n = 4, 2 cannot have an inverse, because 2 multiplied by any integer is even, and thus cannot be equal to 1 + 4z which is odd. To understand when an ...
GRE Math Review 1 Arithmetic
... remainder, where both are integers. Each view is useful, depending on the context. Fractions and decimals are useful when the result must be viewed as a single number, while quotients with remainders are useful for describing the result in terms of integers only. ...
... remainder, where both are integers. Each view is useful, depending on the context. Fractions and decimals are useful when the result must be viewed as a single number, while quotients with remainders are useful for describing the result in terms of integers only. ...
41(3)
... AURORA, SD 57002-0320. E-mails [email protected]. Requests for reprint permission should be directed to the editor. However, general permission is granted to members of The Fibonacci Association for noncommercial reproduction of a limited quantity of individual articles (in whole or in part) provid ...
... AURORA, SD 57002-0320. E-mails [email protected]. Requests for reprint permission should be directed to the editor. However, general permission is granted to members of The Fibonacci Association for noncommercial reproduction of a limited quantity of individual articles (in whole or in part) provid ...
Sequences and Series - Shakopee Public Schools
... equilateral triangle from the center, and repeating for each new triangle. Find the number of triangles in the next 2 iterations. By removing the center of each triangle, each iteration turns every triangle into 3 smaller triangles. So the number of triangles triples with each iteration. The number ...
... equilateral triangle from the center, and repeating for each new triangle. Find the number of triangles in the next 2 iterations. By removing the center of each triangle, each iteration turns every triangle into 3 smaller triangles. So the number of triangles triples with each iteration. The number ...
Generalized Partitions and New Ideas On Number
... The partition function P(n) is defined as the number of ways that a positive integer can be expressed as the sum of positive integers. Two partitions are not considered different if they differ only in the order of their summands. Many results concerning the partition function were discovered using ...
... The partition function P(n) is defined as the number of ways that a positive integer can be expressed as the sum of positive integers. Two partitions are not considered different if they differ only in the order of their summands. Many results concerning the partition function were discovered using ...
Collatz conjecture

The Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse), or the Syracuse problem; the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers (because the values are usually subject to multiple descents and ascents like hailstones in a cloud), or as wondrous numbers.Take any natural number n. If n is even, divide it by 2 to get n / 2. If n is odd, multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process (which has been called ""Half Or Triple Plus One"", or HOTPO) indefinitely. The conjecture is that no matter what number you start with, you will always eventually reach 1. The property has also been called oneness.Paul Erdős said about the Collatz conjecture: ""Mathematics may not be ready for such problems."" He also offered $500 for its solution.