At x - Year11IB
... (x – 1) is not a factor Try (x + 1): Test P(-1) = (-1)3 + 4(-1)2 – 7(-1) – 10 = 0 (x + 1) is a factor Try (x – 2): Test P(2) = (2)3 + 4(2)2 – 7(2) – 10 = 0 (x - 2) is a factor If (x + 1) and (x – 2) are factors then (x + 5) must be the third factor (1 x –2 x 5 = -10) ...
... (x – 1) is not a factor Try (x + 1): Test P(-1) = (-1)3 + 4(-1)2 – 7(-1) – 10 = 0 (x + 1) is a factor Try (x – 2): Test P(2) = (2)3 + 4(2)2 – 7(2) – 10 = 0 (x - 2) is a factor If (x + 1) and (x – 2) are factors then (x + 5) must be the third factor (1 x –2 x 5 = -10) ...
Newton*s second law of motion - crypt
... oscillators such as the pendulum and the mass on spring • Use equations in problem solving ...
... oscillators such as the pendulum and the mass on spring • Use equations in problem solving ...
Math III, Unit 2, Lesson 2
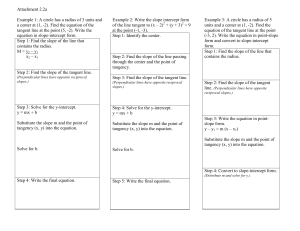
... equation of the tangent line at the point (-3, 2). Write the equation in point-slope form and convert to slope-intercept form. Step 1: Find the slope of the line that contains the radius. ...
... equation of the tangent line at the point (-3, 2). Write the equation in point-slope form and convert to slope-intercept form. Step 1: Find the slope of the line that contains the radius. ...
Sec 4.1 Notes
... In a similar fashion to what you found in the last section, use of the addition method to combine two equations might lead you to results like … 5 = 5 (which is always true, thus indicating that there are infinitely many solutions, since the two equations represent the same line), or 0 = 6 (which is ...
... In a similar fashion to what you found in the last section, use of the addition method to combine two equations might lead you to results like … 5 = 5 (which is always true, thus indicating that there are infinitely many solutions, since the two equations represent the same line), or 0 = 6 (which is ...