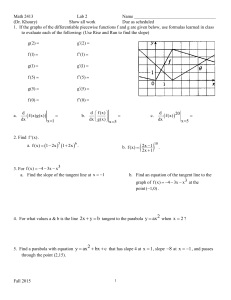
Summer, 2007 – Exam 1 Solutions
... Solution: The auxiliary equation is r2 + 9 = 0. Its solutions are x = ±3i. Therefore, the homogeneous solution is: yh (x) = c1 cos 2x + c2 sin 3x To obtain the particular solution, we use the method of undetermined coefficients. The guess for the particular solution in this case is: yp (x) = x(A cos ...
... Solution: The auxiliary equation is r2 + 9 = 0. Its solutions are x = ±3i. Therefore, the homogeneous solution is: yh (x) = c1 cos 2x + c2 sin 3x To obtain the particular solution, we use the method of undetermined coefficients. The guess for the particular solution in this case is: yp (x) = x(A cos ...
Differential Equations - The University of Texas at Dallas
... For every point P(x, y) on a curve in the first quadrant, the rectangle containing the points O(0, 0) and P(x, y) as vertices is divided by the curve into two regions: upper region A and lower region B. If the curve contains the point Q(1, 3), and region A always has twice the area of region B, find ...
... For every point P(x, y) on a curve in the first quadrant, the rectangle containing the points O(0, 0) and P(x, y) as vertices is divided by the curve into two regions: upper region A and lower region B. If the curve contains the point Q(1, 3), and region A always has twice the area of region B, find ...
Section 10.5, The Polar Coordinate System
... Similarly to graphing in rectangular coordinates, we can use several values of θ to see what value is given for r, then graph the function: θ r ...
... Similarly to graphing in rectangular coordinates, we can use several values of θ to see what value is given for r, then graph the function: θ r ...
Differential equation

A differential equation is a mathematical equation that relates some function with its derivatives. In applications, the functions usually represent physical quantities, the derivatives represent their rates of change, and the equation defines a relationship between the two. Because such relations are extremely common, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.In pure mathematics, differential equations are studied from several different perspectives, mostly concerned with their solutions—the set of functions that satisfy the equation. Only the simplest differential equations are solvable by explicit formulas; however, some properties of solutions of a given differential equation may be determined without finding their exact form.If a self-contained formula for the solution is not available, the solution may be numerically approximated using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have been developed to determine solutions with a given degree of accuracy.