Algebra Lessons: Chapter 5
... DO NOT write on the test. It is a class set to be used for all classes ___________________________________________________________________________________________ Algebra Thursday 02-05-09 Lesson Title: Review and Grade Ch5- Quiz 1 ...
... DO NOT write on the test. It is a class set to be used for all classes ___________________________________________________________________________________________ Algebra Thursday 02-05-09 Lesson Title: Review and Grade Ch5- Quiz 1 ...
Unit 1: Lesson 1 (Gold 1
... Term – a number, variable, or the product of numbers and variables – a part of a variable expression ex. n 6x – y 8x2 + 3x – 4 (1, 2, & 3 terms respectively) Equations – a mathematical sentence that shows that two expressions have the same value ex. – n = 5 6x – y = 7y 8x2 + 3x – 4 = 0 Simplify: Rep ...
... Term – a number, variable, or the product of numbers and variables – a part of a variable expression ex. n 6x – y 8x2 + 3x – 4 (1, 2, & 3 terms respectively) Equations – a mathematical sentence that shows that two expressions have the same value ex. – n = 5 6x – y = 7y 8x2 + 3x – 4 = 0 Simplify: Rep ...
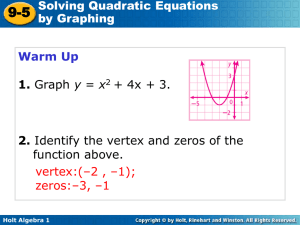
quadratic equation
... equation. A quadratic equation is an equation that can be written in the standard form ax2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. When writing a quadratic function as its related quadratic equation, you replace y with 0. So y = 0. y = ax2 + bx + c 0 = ax2 + bx + c ax2 + bx + c = ...
... equation. A quadratic equation is an equation that can be written in the standard form ax2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. When writing a quadratic function as its related quadratic equation, you replace y with 0. So y = 0. y = ax2 + bx + c 0 = ax2 + bx + c ax2 + bx + c = ...
Unit 6 Study Guide
... 2. _numerical_ _expression__: A mathematical statement including numbers and operations. 3. algebraic___ _expression__: A group of numbers, symbols, and variables that express an operation or a series of operations. 4. _coefficient_____: A numerical factor in a term of an algebraic expression. 5_Dis ...
... 2. _numerical_ _expression__: A mathematical statement including numbers and operations. 3. algebraic___ _expression__: A group of numbers, symbols, and variables that express an operation or a series of operations. 4. _coefficient_____: A numerical factor in a term of an algebraic expression. 5_Dis ...
Euler-Cauchy Equations
... Comment 1: The solution for x < 0 can be obtained from that of x > 0 by replacing x by −x everywhere. Comment 2: Homogeneous Euler-Cauchy equation can be transformed to linear constant coefficient homogeneous equation by changing the independent variable to t = ln x for x > 0. Comment 3: This can be ...
... Comment 1: The solution for x < 0 can be obtained from that of x > 0 by replacing x by −x everywhere. Comment 2: Homogeneous Euler-Cauchy equation can be transformed to linear constant coefficient homogeneous equation by changing the independent variable to t = ln x for x > 0. Comment 3: This can be ...
High School Math 2 Unit 1: Extending the Number System
... N.RN.2 Rewrite expressions involving radicals and rational exponents using the properties of exponents. Use properties of rational and irrational numbers. N.RN.3 Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irra ...
... N.RN.2 Rewrite expressions involving radicals and rational exponents using the properties of exponents. Use properties of rational and irrational numbers. N.RN.3 Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irra ...
(pdf)
... We will need the following short notation. P Definition 5. For m ∈ N, denote σ1 (m) = d|m d. In order to prove that j(z0 ) is an algebraic number when z0 is a complex modulus, we would construct a particular polynomial with a root j(z0 ). To do this we would first need the following more general res ...
... We will need the following short notation. P Definition 5. For m ∈ N, denote σ1 (m) = d|m d. In order to prove that j(z0 ) is an algebraic number when z0 is a complex modulus, we would construct a particular polynomial with a root j(z0 ). To do this we would first need the following more general res ...
Revised Version 070216
... properties of exponents, we can conclude that i 2 = e 4 . In this € way, if we let ...
... properties of exponents, we can conclude that i 2 = e 4 . In this € way, if we let ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.