Linear Algebra Review
... It turns out the same idea works for computers. Computer algorithms for generating primes p and q and forming m pq are astronomically faster than starting with m and factoring to find the primes p and q that produced it. This assumes of course that the primes p and q are sufficiently large. Howeve ...
... It turns out the same idea works for computers. Computer algorithms for generating primes p and q and forming m pq are astronomically faster than starting with m and factoring to find the primes p and q that produced it. This assumes of course that the primes p and q are sufficiently large. Howeve ...
THE DIFFERENT IDEAL 1. Introduction O
... divide 1. Therefore it remains to check the two divisibility relations. To show pe−1 | DK , write (p) = pe−1 a. Since pe | (p), p | a. To say pe−1 | DK is equivalent, by Lemma 4.7, to saying TrK/Q (p−(e−1) ) ⊂ Z. Since p−(e−1) = p1 a, TrK/Q (p−(e−1) ) ⊂ Z if and only if TrK/Q (a) ⊂ pZ, which is the ...
... divide 1. Therefore it remains to check the two divisibility relations. To show pe−1 | DK , write (p) = pe−1 a. Since pe | (p), p | a. To say pe−1 | DK is equivalent, by Lemma 4.7, to saying TrK/Q (p−(e−1) ) ⊂ Z. Since p−(e−1) = p1 a, TrK/Q (p−(e−1) ) ⊂ Z if and only if TrK/Q (a) ⊂ pZ, which is the ...
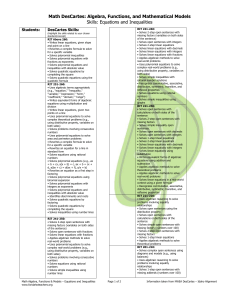
Math Algebra Plannin..
... • Solves polynomial equations (e.g., ax = b + cx, a(x + b) = c, ax + b = cx + d, a(bx + c) = d(ex + f), a/x = b) • Rewrites an equation as a first step in factoring • Solves polynomial equations using binomial expansion • Solves polynomial equations with integers as exponents • Solves polynomial equ ...
... • Solves polynomial equations (e.g., ax = b + cx, a(x + b) = c, ax + b = cx + d, a(bx + c) = d(ex + f), a/x = b) • Rewrites an equation as a first step in factoring • Solves polynomial equations using binomial expansion • Solves polynomial equations with integers as exponents • Solves polynomial equ ...
MTH 05 Lecture Notes
... the denominator is called a proper fraction. For this reason, a fraction whose numerator is greater than or equal to the denominator is sometimes called an improper fraction. However, there is nothing improper about improper fractions at all—we will work with them routinely. In fact, in most circums ...
... the denominator is called a proper fraction. For this reason, a fraction whose numerator is greater than or equal to the denominator is sometimes called an improper fraction. However, there is nothing improper about improper fractions at all—we will work with them routinely. In fact, in most circums ...
last updated 2012-02-25 with Set 8
... already know that the (usually infinite) product ζA (s) converges absolutely when Re(s) is sufficiently large.) Suggestion of the proof. Use induction on n and the result on ζFq [T ] (s) in Problem 29. 33. By using Problem 32, prove that for any commutative ring A which is finitely generated over Z, ...
... already know that the (usually infinite) product ζA (s) converges absolutely when Re(s) is sufficiently large.) Suggestion of the proof. Use induction on n and the result on ζFq [T ] (s) in Problem 29. 33. By using Problem 32, prove that for any commutative ring A which is finitely generated over Z, ...
41(4)
... This solution can also be derived from Theorem 1 since the characteristic polynomial has the decomposition (5). Since the DIFS of order (r^r) is the r-fold convolution of DIFS of order ...
... This solution can also be derived from Theorem 1 since the characteristic polynomial has the decomposition (5). Since the DIFS of order (r^r) is the r-fold convolution of DIFS of order ...
Ex3 - WordPress.com
... Q5. Write the smallest 5- digit number and express it in the terms of its prime factors. Q6. Find all the factors 1729 and arrange them in ascending order. Now state the relation, if any; between two consecutive prime factors. Q7. The product of three consecutive numbers is always divisible by 6.Ve ...
... Q5. Write the smallest 5- digit number and express it in the terms of its prime factors. Q6. Find all the factors 1729 and arrange them in ascending order. Now state the relation, if any; between two consecutive prime factors. Q7. The product of three consecutive numbers is always divisible by 6.Ve ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.