Parent Letter September-October Transitions
... If you complete the square for the general equation ax2 bx c 0, you get the Quadratic Formula: If ax2 bx c 0, then the solutions are x ...
... If you complete the square for the general equation ax2 bx c 0, you get the Quadratic Formula: If ax2 bx c 0, then the solutions are x ...
Homework Sheet Section 1
... for women: “Give yourself 100 pounds for the first 5 feet plus 5 pounds for every inch over 5 feet tall.” Using this description, what height corresponds to a recommended weight of 135 pounds? 2. Perform the indicated operations and write the result in standard form: ...
... for women: “Give yourself 100 pounds for the first 5 feet plus 5 pounds for every inch over 5 feet tall.” Using this description, what height corresponds to a recommended weight of 135 pounds? 2. Perform the indicated operations and write the result in standard form: ...
Full text
... where £(/c) = 1,6, 42, and 15 when k = 3, 7, 49, and 31, respectively. Note that i denotes the square root of -1 in the last formula. It is perhaps clear that the determination of such asymptotic formulas involves sums of complex expressions dependent on the orbit of 10 modulo k9 ...
... where £(/c) = 1,6, 42, and 15 when k = 3, 7, 49, and 31, respectively. Note that i denotes the square root of -1 in the last formula. It is perhaps clear that the determination of such asymptotic formulas involves sums of complex expressions dependent on the orbit of 10 modulo k9 ...
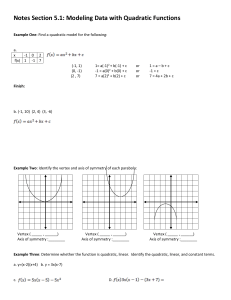
Notes Section 5.1: Modeling Data with Quadratic Functions Example
... 3) Fill in the information about the quadratic, and then graph the parabola. ...
... 3) Fill in the information about the quadratic, and then graph the parabola. ...
Chapter Five: Quadratic Functions Section One: Introduction to
... 1. Plug the three points into the standard form of the equation: y ax 2 bx c 2. You should now have three equations with three variables: a, b, and c 3. Solve the system for the missing variables 4. Plug these values back into y ax 2 bx c EX1: Find the quadratic function whose graph cont ...
... 1. Plug the three points into the standard form of the equation: y ax 2 bx c 2. You should now have three equations with three variables: a, b, and c 3. Solve the system for the missing variables 4. Plug these values back into y ax 2 bx c EX1: Find the quadratic function whose graph cont ...
Section 11.2 - MiraCosta College
... 11.2 The Quadratic Formula Solving Quadratic Equations Using the Quadratic Formula. By solving the general quadratic equation ax2 + bx + c = 0 using the method of completing the square, one can derive the quadratic formula. The quadratic formula can be used to solve any quadratic equation. The Quadr ...
... 11.2 The Quadratic Formula Solving Quadratic Equations Using the Quadratic Formula. By solving the general quadratic equation ax2 + bx + c = 0 using the method of completing the square, one can derive the quadratic formula. The quadratic formula can be used to solve any quadratic equation. The Quadr ...
Scheme of work for Unit 3 Modular Exam (Number, Shape Space
... Understanding that ‘percentage’ means ‘number of parts per 100’ and use this to compare proportions Interpreting percentage as the operator 'so many hundredths of' Multiplying and dividing numbers with no more than one decimal digit, using the commutative, associative, and distributive laws an ...
... Understanding that ‘percentage’ means ‘number of parts per 100’ and use this to compare proportions Interpreting percentage as the operator 'so many hundredths of' Multiplying and dividing numbers with no more than one decimal digit, using the commutative, associative, and distributive laws an ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.