Document
... When working with negative radicands, use the definition before using any of the other rules for radicals. In particular, the rule is valid only when c and d are not both negative. For example while ...
... When working with negative radicands, use the definition before using any of the other rules for radicals. In particular, the rule is valid only when c and d are not both negative. For example while ...
36 it follows that x4 − x2 + 2 ̸= 0. 11. Proof. Consider the number
... a2 = 6b2 = 2(3b2 ). Because 3b2 is an integer, a2 is even. Thus a is even. So a = 2c, where c ∈ Z. Thus (2c)2 = 6b2 and so 4c2 = 6b2 . Therefore, 3b2 = 2c2 . Because c2 is an integer, 3b2 is even. Thus either 3 is even or b2 is even. Since 3 is not even, b2 is even and so b is even. However, since a ...
... a2 = 6b2 = 2(3b2 ). Because 3b2 is an integer, a2 is even. Thus a is even. So a = 2c, where c ∈ Z. Thus (2c)2 = 6b2 and so 4c2 = 6b2 . Therefore, 3b2 = 2c2 . Because c2 is an integer, 3b2 is even. Thus either 3 is even or b2 is even. Since 3 is not even, b2 is even and so b is even. However, since a ...
Unit 1: Extending the Number System
... properties of circles, including central and inscribed angles, chords of a circle, and tangents of a circle. Then you build on this to explore polygons circumscribed and inscribed in a circle. You will then learn about the properties and construction of tangent lines. The measurement units of radian ...
... properties of circles, including central and inscribed angles, chords of a circle, and tangents of a circle. Then you build on this to explore polygons circumscribed and inscribed in a circle. You will then learn about the properties and construction of tangent lines. The measurement units of radian ...
F COMPLEX NUMBERS
... This root√is a real number, but it is expressed by a formula that involves the complex number −3. So we find, surprisingly, that even if we wanted to restrict ourselves to real roots of equations, we would still need complex numbers to write down those roots. Since there was no escape, mathematician ...
... This root√is a real number, but it is expressed by a formula that involves the complex number −3. So we find, surprisingly, that even if we wanted to restrict ourselves to real roots of equations, we would still need complex numbers to write down those roots. Since there was no escape, mathematician ...
Math 1311 – Business Math I
... xn : exponential notation, x is called the ___________ and n is called the ____________ or the ___________ and xn = xxxx … x ( a total of n x’s) – this is the expanded notation ...
... xn : exponential notation, x is called the ___________ and n is called the ____________ or the ___________ and xn = xxxx … x ( a total of n x’s) – this is the expanded notation ...
Document
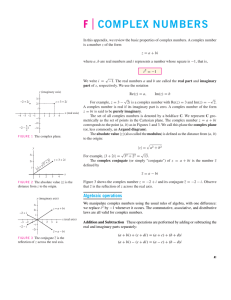
... Complex numbers can be defined as ordered pairs (x,y) of real numbers that are to be interpreted as points in the complex plane, with rectangular coordinates x and y, just as real numbers x are thought of as points on the ...
... Complex numbers can be defined as ordered pairs (x,y) of real numbers that are to be interpreted as points in the complex plane, with rectangular coordinates x and y, just as real numbers x are thought of as points on the ...