An Invitation to Sample Paths of Brownian Motion
... 3.1. Definition. Standard Brownian motion on an interval I = [0, a] or I = [0, ∞) is defined by the following properties: Definition 3.1. A real-valued stochastic process {Bt }t∈I is a standard Brownian motion if it is a Gaussian process such that: (i) B0 = 0, (ii) ∀k natural and ∀t1 < . . . < tk in ...
... 3.1. Definition. Standard Brownian motion on an interval I = [0, a] or I = [0, ∞) is defined by the following properties: Definition 3.1. A real-valued stochastic process {Bt }t∈I is a standard Brownian motion if it is a Gaussian process such that: (i) B0 = 0, (ii) ∀k natural and ∀t1 < . . . < tk in ...
Measure Theoretic Probability P.J.C. Spreij (minor revisions by S.G.
... In these notes we explain the measure theoretic foundations of modern probability. The notes are used during a course that had as one of its principal aims a swift introduction to measure theory as far as it is needed in modern probability, e.g. to define concepts as conditional expectation and to p ...
... In these notes we explain the measure theoretic foundations of modern probability. The notes are used during a course that had as one of its principal aims a swift introduction to measure theory as far as it is needed in modern probability, e.g. to define concepts as conditional expectation and to p ...
Notes on stochastic processes
... A stochastic or random process is a collection of random variables that is indexed by or depends on some mathematical set [120, page 7][67, page 1]. More formally, a stochastic process is defined as a collection of random variables defined on a common probability space (P, F, Ω), where P is a probab ...
... A stochastic or random process is a collection of random variables that is indexed by or depends on some mathematical set [120, page 7][67, page 1]. More formally, a stochastic process is defined as a collection of random variables defined on a common probability space (P, F, Ω), where P is a probab ...
here for U12 text. - Iowa State University
... fundamental theory on which the simplest model of a repairable component is based. Section 12.3 presents the special case of the Poisson process, based on exponentially distributed inter-failure times. Section 12.4 introduces the alternating renewal process so as to address the case of non-zero repa ...
... fundamental theory on which the simplest model of a repairable component is based. Section 12.3 presents the special case of the Poisson process, based on exponentially distributed inter-failure times. Section 12.4 introduces the alternating renewal process so as to address the case of non-zero repa ...
PARTITION STATISTICS EQUIDISTRIBUTED WITH THE NUMBER OF HOOK DIFFERENCE ONE CELLS
... the k-th (↵, )-diagonal length, denoted by dk ( ). We call the sequence {dk ( )} the (↵, )-diagonal pattern of . (The modifier (↵, ) is dropped if it is clear in context.) In the case ↵ = m 1, = 1, we change the modifier (↵, ) to m. • Let ↵, be non-negative integers, not both zero. Define H↵, ( ) = ...
... the k-th (↵, )-diagonal length, denoted by dk ( ). We call the sequence {dk ( )} the (↵, )-diagonal pattern of . (The modifier (↵, ) is dropped if it is clear in context.) In the case ↵ = m 1, = 1, we change the modifier (↵, ) to m. • Let ↵, be non-negative integers, not both zero. Define H↵, ( ) = ...
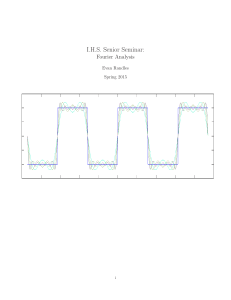
IHS Senior Seminar - UCLA Department of Mathematics
... each ǫ > 0, there is N = N (x, ǫ) ∈ N such that |fn (x) − f (x)| < ǫ for all n ≥ N . Notice the order of quantifiers in this statement. We first talk about a point x and then talk about a limit. The next definition, which is a stronger notion of the one above, moves the x-quantifier. Definition 2.9 ...
... each ǫ > 0, there is N = N (x, ǫ) ∈ N such that |fn (x) − f (x)| < ǫ for all n ≥ N . Notice the order of quantifiers in this statement. We first talk about a point x and then talk about a limit. The next definition, which is a stronger notion of the one above, moves the x-quantifier. Definition 2.9 ...
Views of Pi: definition and computation
... There are several approaches to the π number. This variety of approaches imposes a dilemma on the teacher or the developer of a formalized mathematics library: what should be used as the definition, and what should be understood as provable properties of the number? The investigations in this paper ...
... There are several approaches to the π number. This variety of approaches imposes a dilemma on the teacher or the developer of a formalized mathematics library: what should be used as the definition, and what should be understood as provable properties of the number? The investigations in this paper ...
The k-Binomial Transforms and the Hankel Transform
... The numbers in the triangle described in Lemma 2.1, not just the right and left diagonals, can also have combinatorial interpretations. For instance, the triangle of numbers in Figure 1 ...
... The numbers in the triangle described in Lemma 2.1, not just the right and left diagonals, can also have combinatorial interpretations. For instance, the triangle of numbers in Figure 1 ...
Measure Theoretic Probability P.J.C. Spreij
... The proof of this theorem is deferred to later, see Theorem 2.6. For the time being, we take this existence result for granted. One remark is in order. One can show that B is not the largest σ-algebra for which the measure λ can coherently be defined. On the other hand, on the power set of R it is i ...
... The proof of this theorem is deferred to later, see Theorem 2.6. For the time being, we take this existence result for granted. One remark is in order. One can show that B is not the largest σ-algebra for which the measure λ can coherently be defined. On the other hand, on the power set of R it is i ...
Errors and Floating Point
... be introduced at this stage. In general, we can say that Error = True value – Approximate value. The errors may be divided into the following different types: 1. Inherent Error: The inherent error is that quantity which is already present in the statement of the problem before its solution. The inhe ...
... be introduced at this stage. In general, we can say that Error = True value – Approximate value. The errors may be divided into the following different types: 1. Inherent Error: The inherent error is that quantity which is already present in the statement of the problem before its solution. The inhe ...