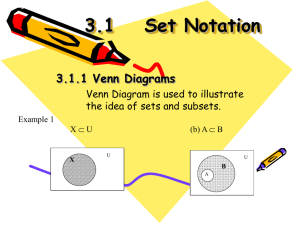
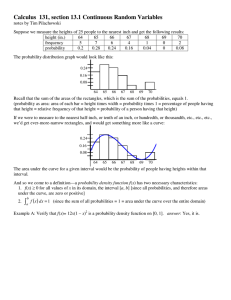
Lecture 8. Random Variables (continued), Expected Value, Variance
... behavior of a function, we mean properties of the function that cannot be observed except by surveying its entire domain.) For example, to compute P (X = x), we work with the set { ω ∈ Ω | X(ω) = x }. We can never find out anything about this set by evaluating X at one element of Ω. To create a list ...
... behavior of a function, we mean properties of the function that cannot be observed except by surveying its entire domain.) For example, to compute P (X = x), we work with the set { ω ∈ Ω | X(ω) = x }. We can never find out anything about this set by evaluating X at one element of Ω. To create a list ...
Word
... this result purely by deductive reasoning. The result does not require that any coin be tossed (after all, it’s common sense right?). Nothing is said, however, about how one can determine whether or not a particular coin is true/fair. Unfortunately, there are some rather troublesome defects in the c ...
... this result purely by deductive reasoning. The result does not require that any coin be tossed (after all, it’s common sense right?). Nothing is said, however, about how one can determine whether or not a particular coin is true/fair. Unfortunately, there are some rather troublesome defects in the c ...
Worksheet - WordPress.com
... A speaks truth in 75% of cases and B in 80% of cases. In what percent of cases are they likely to contradict each other in narrating the same event? A. 35% B. 5% C. 45% D. 22.5% ...
... A speaks truth in 75% of cases and B in 80% of cases. In what percent of cases are they likely to contradict each other in narrating the same event? A. 35% B. 5% C. 45% D. 22.5% ...
Number of times resulting in event Total number of times experiment
... Random Phenomenon is a situation in which we know what outcomes can occur, but we do not know which outcome will occur. We cannot predict each outcome, but there will be a regular distribution over many repetitions. ...
... Random Phenomenon is a situation in which we know what outcomes can occur, but we do not know which outcome will occur. We cannot predict each outcome, but there will be a regular distribution over many repetitions. ...
August 2016 COSC 412 Discrete probability Discrete probability
... In everyday discussions about probability we don’t really tend to think about distributions but rather about events whose outcome is uncertain. So when we say “The chance of rolling a 6 on a fair die is 1/6” we are thinking about a random variable, R (the result of rolling a fair die), and the proba ...
... In everyday discussions about probability we don’t really tend to think about distributions but rather about events whose outcome is uncertain. So when we say “The chance of rolling a 6 on a fair die is 1/6” we are thinking about a random variable, R (the result of rolling a fair die), and the proba ...
AA2 Chapter 7 and 11 Quiz REVIEW
... 8. Determine whether the following problem involves a permutation or combination: A medical researcher needs 13 people to test the effectiveness of an experimental drug. If 29 people have volunteered for the test, in how many ways can 13 people be selected? Don’t solve the problem. ...
... 8. Determine whether the following problem involves a permutation or combination: A medical researcher needs 13 people to test the effectiveness of an experimental drug. If 29 people have volunteered for the test, in how many ways can 13 people be selected? Don’t solve the problem. ...
2-2 Distributive Property
... McCutchen’s next hit is a 2B. In other words, the P(2B | Hit). P(2B | Hit) = P(Hit and 2B) P(Hit) As of 5/11/17 his P(Hit and 2B) is .0413 P(Hit) is .215 .0413 ÷ .215 = .1922 or about a 19% chance that his next hit is a 2B ...
... McCutchen’s next hit is a 2B. In other words, the P(2B | Hit). P(2B | Hit) = P(Hit and 2B) P(Hit) As of 5/11/17 his P(Hit and 2B) is .0413 P(Hit) is .215 .0413 ÷ .215 = .1922 or about a 19% chance that his next hit is a 2B ...
Infinite monkey theorem

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare.In this context, ""almost surely"" is a mathematical term with a precise meaning, and the ""monkey"" is not an actual monkey, but a metaphor for an abstract device that produces an endless random sequence of letters and symbols. One of the earliest instances of the use of the ""monkey metaphor"" is that of French mathematician Émile Borel in 1913, but the first instance may be even earlier. The relevance of the theorem is questionable—the probability of a universe full of monkeys typing a complete work such as Shakespeare's Hamlet is so tiny that the chance of it occurring during a period of time hundreds of thousands of orders of magnitude longer than the age of the universe is extremely low (but technically not zero). It should also be noted that real monkeys don't produce uniformly random output, which means that an actual monkey hitting keys for an infinite amount of time has no statistical certainty of ever producing any given text.Variants of the theorem include multiple and even infinitely many typists, and the target text varies between an entire library and a single sentence. The history of these statements can be traced back to Aristotle's On Generation and Corruption and Cicero's De natura deorum (On the Nature of the Gods), through Blaise Pascal and Jonathan Swift, and finally to modern statements with their iconic simians and typewriters. In the early 20th century, Émile Borel and Arthur Eddington used the theorem to illustrate the timescales implicit in the foundations of statistical mechanics.