- Wiley Online Library
... The method was further generalized to improve performance for a wider class of problems, such as using hypergeometric polynomials from the Askey scheme to obtain exponential convergence rate for non-Gaussian random processes [7], wavelet-based Weiner–Haar basis to deal with sharp or even discontinuo ...
... The method was further generalized to improve performance for a wider class of problems, such as using hypergeometric polynomials from the Askey scheme to obtain exponential convergence rate for non-Gaussian random processes [7], wavelet-based Weiner–Haar basis to deal with sharp or even discontinuo ...
108_01_basics
... Able to tell what an algorithm is and have some understanding why we study algorithms ...
... Able to tell what an algorithm is and have some understanding why we study algorithms ...
Likelihood inference for generalized Pareto distribution
... Davison, A. C.; Smith, R. L. (1990). Models for exceedances over high thresholds. With discussion and a reply by the authors. JRSS-B Embrechts, P. Klüppelberg, C. and Mikosch, T. (1997). Modelling Extremal Events for Insurance and Finance. Springer-Verlag, Berlin. McNeil, A. J., Frey, R. and Embrec ...
... Davison, A. C.; Smith, R. L. (1990). Models for exceedances over high thresholds. With discussion and a reply by the authors. JRSS-B Embrechts, P. Klüppelberg, C. and Mikosch, T. (1997). Modelling Extremal Events for Insurance and Finance. Springer-Verlag, Berlin. McNeil, A. J., Frey, R. and Embrec ...
The problems in this booklet are organized into strands. A
... First we should determine the number of three digit integers greater than or equal to 100. The number 999 is the largest three digit number so from 1 to 999 there are 999 numbers. This includes 99 numbers from 1 to 99 that must be excluded. So there are 999 − 99 = 900 three digit numbers. We now mus ...
... First we should determine the number of three digit integers greater than or equal to 100. The number 999 is the largest three digit number so from 1 to 999 there are 999 numbers. This includes 99 numbers from 1 to 99 that must be excluded. So there are 999 − 99 = 900 three digit numbers. We now mus ...
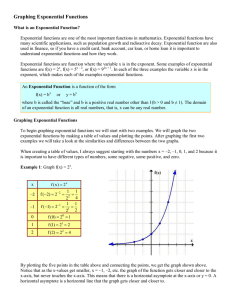
Graphing Exponential Functions
... where b is called the “base” and b is a positive real number other than 1(b > 0 and b ≠ 1). The domain of an exponential function is all real numbers, that is, x can be any real number. Graphing Exponential Functions To begin graphing exponential functions we will start with two examples. We will ...
... where b is called the “base” and b is a positive real number other than 1(b > 0 and b ≠ 1). The domain of an exponential function is all real numbers, that is, x can be any real number. Graphing Exponential Functions To begin graphing exponential functions we will start with two examples. We will ...
Best Keyword Cover Search
... In keyword-NNE algorithm, the best-first browsing strategy is applied like BF-baseline but large memory requirement is avoided. For the better explanation, we can imagine all candidate keyword covers generated in BF-baseline algorithm are grouped into independent groups. Each group is associated wit ...
... In keyword-NNE algorithm, the best-first browsing strategy is applied like BF-baseline but large memory requirement is avoided. For the better explanation, we can imagine all candidate keyword covers generated in BF-baseline algorithm are grouped into independent groups. Each group is associated wit ...
Document
... • m-2k times: each occurrence of x in A that is not paired by another x (there are k pairs xx in A, thus m-2k of other occurrences of x in A) is paired by some other value (different than x) which gives at least 2k+(m-2k) = m occurrences in total, and contradicts the fact that x is a majority in A. ...
... • m-2k times: each occurrence of x in A that is not paired by another x (there are k pairs xx in A, thus m-2k of other occurrences of x in A) is paired by some other value (different than x) which gives at least 2k+(m-2k) = m occurrences in total, and contradicts the fact that x is a majority in A. ...
Travelling salesman problem
The travelling salesman problem (TSP) asks the following question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city? It is an NP-hard problem in combinatorial optimization, important in operations research and theoretical computer science.TSP is a special case of the travelling purchaser problem and the Vehicle routing problem.In the theory of computational complexity, the decision version of the TSP (where, given a length L, the task is to decide whether the graph has any tour shorter than L) belongs to the class of NP-complete problems. Thus, it is possible that the worst-case running time for any algorithm for the TSP increases superpolynomially (perhaps, specifically, exponentially) with the number of cities.The problem was first formulated in 1930 and is one of the most intensively studied problems in optimization. It is used as a benchmark for many optimization methods. Even though the problem is computationally difficult, a large number of heuristics and exact methods are known, so that some instances with tens of thousands of cities can be solved completely and even problems with millions of cities can be approximated within a small fraction of 1%.The TSP has several applications even in its purest formulation, such as planning, logistics, and the manufacture of microchips. Slightly modified, it appears as a sub-problem in many areas, such as DNA sequencing. In these applications, the concept city represents, for example, customers, soldering points, or DNA fragments, and the concept distance represents travelling times or cost, or a similarity measure between DNA fragments. The TSP also appears in astronomy, as astronomers observing many sources will want to minimise the time spent slewing the telescope between the sources. In many applications, additional constraints such as limited resources or time windows may be imposed.