Note on the convex hull of the Stiefel manifold - FSU Math
... Let p and n be positive integers with p ≤ n. The (compact) Stiefel manifold is the set St(p, n) = {X ∈ Rn×p : X T X = Ip }, where Ip denotes the identity matrix of size p. We view St(p, n) as a subset of Rn×p endowed with the Frobenius norm. The fact that St(p, n) has a natural manifold structure is ...
... Let p and n be positive integers with p ≤ n. The (compact) Stiefel manifold is the set St(p, n) = {X ∈ Rn×p : X T X = Ip }, where Ip denotes the identity matrix of size p. We view St(p, n) as a subset of Rn×p endowed with the Frobenius norm. The fact that St(p, n) has a natural manifold structure is ...
Linear Maps - People Pages - University of Wisconsin
... Example 1.18. Find a basis of the kernel and image in example (1.4). Recall that T (x1 , x2 , x3 ) = (3x1 − x3 , 5x1 + 2x2 − 4x3 ), so (x1 , x2 , x3 , x4 ) ∈ ker(T ) if and only if 3x1 − x3 = 0 5x1 + 2x2 − 4x3 = 0. We already know how to solve this system of equations. We can rewrite the solution in ...
... Example 1.18. Find a basis of the kernel and image in example (1.4). Recall that T (x1 , x2 , x3 ) = (3x1 − x3 , 5x1 + 2x2 − 4x3 ), so (x1 , x2 , x3 , x4 ) ∈ ker(T ) if and only if 3x1 − x3 = 0 5x1 + 2x2 − 4x3 = 0. We already know how to solve this system of equations. We can rewrite the solution in ...
Math 215A HW3 Solution to Problem 1
... In this section we make use of the following lemmata: Lemmata 1. Let G be a topological group with a normal subgroup H. Then if H and G/H are connected, then so is G. Proof. Suppose that G is not connected, i.e. G = M ∪ N where M, N are open and M ∩ N = S ∅. Now it is clear that G = g∈G gH, and sinc ...
... In this section we make use of the following lemmata: Lemmata 1. Let G be a topological group with a normal subgroup H. Then if H and G/H are connected, then so is G. Proof. Suppose that G is not connected, i.e. G = M ∪ N where M, N are open and M ∩ N = S ∅. Now it is clear that G = g∈G gH, and sinc ...
Linear Algebra (wi1403lr)
... Proof (by showing equivalence of the two statements) • (a) ⇒ (l): By the third property on the previous slide. • (l) ⇒ (a): By the third property on the previous slide with A and ...
... Proof (by showing equivalence of the two statements) • (a) ⇒ (l): By the third property on the previous slide. • (l) ⇒ (a): By the third property on the previous slide with A and ...
REPRESENTATIONS OF LIE GROUPS AND LIE ALGEBRAS
... with B the transition matrix between the two bases, it follows that the transition maps are smooth. Thus, this smooth manifold structure on GL(V ) is independent of the choice of basis. This Lie group GL(V ) will play an important role in the later sections of this paper. First we review the concept ...
... with B the transition matrix between the two bases, it follows that the transition maps are smooth. Thus, this smooth manifold structure on GL(V ) is independent of the choice of basis. This Lie group GL(V ) will play an important role in the later sections of this paper. First we review the concept ...
Representation Theory Of Algebras Related To The Partition Algebra
... same structure as a given, abstract, group (see, for example, [1]). Formally, a representation of a group is a homomorphism G → GLn (F ) for a field F, giving an invertible n × n matrix for each element of G. More abstractly, representations of a group G may be defined in terms of modules over the g ...
... same structure as a given, abstract, group (see, for example, [1]). Formally, a representation of a group is a homomorphism G → GLn (F ) for a field F, giving an invertible n × n matrix for each element of G. More abstractly, representations of a group G may be defined in terms of modules over the g ...
Bounded operator
... Conversely, it follows from the continuity at the zero vector that there exists a such that for all vectors h in X with . Thus, for all non-zero X, one has ...
... Conversely, it follows from the continuity at the zero vector that there exists a such that for all vectors h in X with . Thus, for all non-zero X, one has ...
Invertible matrix
... Non-square matrices (m-by-n matrices for which m ≠ n) do not have an inverse. However, in some cases such a matrix may have a left inverse or right inverse. If A is m-by-n and the rank of A is equal to n, then A has a left inverse: an n-by-m matrix B such that BA = I. If A has rank m, then it has a ...
... Non-square matrices (m-by-n matrices for which m ≠ n) do not have an inverse. However, in some cases such a matrix may have a left inverse or right inverse. If A is m-by-n and the rank of A is equal to n, then A has a left inverse: an n-by-m matrix B such that BA = I. If A has rank m, then it has a ...
A generalization of the Chandler Davis convexity theorem.
... In this paper we generalize Davis’s theorem to a broader context that includes, most notably, arbitrary groups, non-linear group actions and infinite dimensional spaces. In Davis’s original proof it was important that the rotations act linearly on matrices. Our approach is more general and completel ...
... In this paper we generalize Davis’s theorem to a broader context that includes, most notably, arbitrary groups, non-linear group actions and infinite dimensional spaces. In Davis’s original proof it was important that the rotations act linearly on matrices. Our approach is more general and completel ...
Number of subgroups of index 2.
... To see this, we start by the following observation. If H is a subgroup of index 2 in G, then H is normal in G and the factor group G/H has order 2. Therefore, by a consequence of the Lagrange Theorem [2, Corollary 7.4], (xH)2 = H for all x 2 G. Hence, x2 2 H for all x 2 G, and it follows that G2 ✓ H ...
... To see this, we start by the following observation. If H is a subgroup of index 2 in G, then H is normal in G and the factor group G/H has order 2. Therefore, by a consequence of the Lagrange Theorem [2, Corollary 7.4], (xH)2 = H for all x 2 G. Hence, x2 2 H for all x 2 G, and it follows that G2 ✓ H ...
Algebra I
... steps of simplifying functions and solving equations. AGS Algebra: Chapter 1: Lessons 8-10; Chapter 2: Lessons 1-11; Chapter 3: Lessons 2-6, 10, 11, Application; Chapter 4: Lessons 2-8; Chapter 5: Lessons 6-10; Chapter 8: Lessons 6-9; Chapter 10: Lessons 4, 5 A1.9.4 Understand that the logic of equa ...
... steps of simplifying functions and solving equations. AGS Algebra: Chapter 1: Lessons 8-10; Chapter 2: Lessons 1-11; Chapter 3: Lessons 2-6, 10, 11, Application; Chapter 4: Lessons 2-8; Chapter 5: Lessons 6-10; Chapter 8: Lessons 6-9; Chapter 10: Lessons 4, 5 A1.9.4 Understand that the logic of equa ...
boundary behavior of poisson integrals on symmetric spaces
... fact, by [9] and by some recent, as yet unpublished results of E. M. Stein and N. J. Weiss, even for ¿^functions. In §4 we make some remarks on unrestricted admissible convergence without being able to settle the question completely. In §5 we discuss symmetric spaces of rank one; in this case there ...
... fact, by [9] and by some recent, as yet unpublished results of E. M. Stein and N. J. Weiss, even for ¿^functions. In §4 we make some remarks on unrestricted admissible convergence without being able to settle the question completely. In §5 we discuss symmetric spaces of rank one; in this case there ...
BOUNDED GENERATION OF S-ARITHMETIC SUBGROUPS OF
... Witt index is one due to some technical problems, but mainly because of the fact that the resulting special orthogonal group in dimension n = 5 is no longer split and bounded generation of its S-arithmetic subgroups has not been previously established. At the same time, the method used in [9] does n ...
... Witt index is one due to some technical problems, but mainly because of the fact that the resulting special orthogonal group in dimension n = 5 is no longer split and bounded generation of its S-arithmetic subgroups has not been previously established. At the same time, the method used in [9] does n ...
Stability of closedness of convex cones under linear mappings
... then there exists a neighbourhood W of T in L(Rn , Rm ) such that ker(S) ∩ icor(K) 6= ∅ for all S ∈ W. In particular, S(K) is a closed convex cone in Rm for each S ∈ W. Proof: Let M ⊆ L(Y, Rm ) be the family of all mappings with rank m. It is routine to show that M is a dense open subset of L(Y, Rm ...
... then there exists a neighbourhood W of T in L(Rn , Rm ) such that ker(S) ∩ icor(K) 6= ∅ for all S ∈ W. In particular, S(K) is a closed convex cone in Rm for each S ∈ W. Proof: Let M ⊆ L(Y, Rm ) be the family of all mappings with rank m. It is routine to show that M is a dense open subset of L(Y, Rm ...
Zero products of Toeplitz operators
... We exploit the close relationship of kernels of Toeplitz operators to the so-called nearly invariant subspaces [10]. These are subspaces of H p with the property that each zero of an element in the space which is not a common zero can be divided out without leaving the space. It is wellknown that th ...
... We exploit the close relationship of kernels of Toeplitz operators to the so-called nearly invariant subspaces [10]. These are subspaces of H p with the property that each zero of an element in the space which is not a common zero can be divided out without leaving the space. It is wellknown that th ...
(Non-)Commutative Topology
... From analysis point of view, the discrete topology is the most reasonable topology for a finite set X, and the counting measure is the natural choice for measure theory. We should not endow an infinite set with the discrete topology nor with the counting measure. Instead, non-trivial topology and me ...
... From analysis point of view, the discrete topology is the most reasonable topology for a finite set X, and the counting measure is the natural choice for measure theory. We should not endow an infinite set with the discrete topology nor with the counting measure. Instead, non-trivial topology and me ...
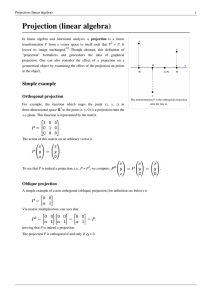
Projection (linear algebra)
... When the underlying vector space X is a (not necessarily finite-dimensional) normed vector space, analytic questions, irrelevant in the finite-dimensional case, need to be considered. Assume now X is a Banach space. Many of the algebraic notions discussed above survive the passage to this context. A ...
... When the underlying vector space X is a (not necessarily finite-dimensional) normed vector space, analytic questions, irrelevant in the finite-dimensional case, need to be considered. Assume now X is a Banach space. Many of the algebraic notions discussed above survive the passage to this context. A ...
CHARACTER THEORY OF COMPACT LIE GROUPS
... order to use the above maps. Once we do, it will turn out that g can be given the structure of a non-associative algebra under the operation [X, Y ] := ad(X)(Y ). In a purely geometrical approach, this corresponds to the Lie derivative of Y with respect to X. For our purposes, this is not a particul ...
... order to use the above maps. Once we do, it will turn out that g can be given the structure of a non-associative algebra under the operation [X, Y ] := ad(X)(Y ). In a purely geometrical approach, this corresponds to the Lie derivative of Y with respect to X. For our purposes, this is not a particul ...
A refinement-based approach to computational algebra in Coq⋆
... This is an implementation of matrix multiplication that is clearly not suited for proving algebraic properties, like associativity. The correctness of this function is expressed by the fact that if f is instantiated by the multiplication of matrices, winograd_step A B should be the product of A and ...
... This is an implementation of matrix multiplication that is clearly not suited for proving algebraic properties, like associativity. The correctness of this function is expressed by the fact that if f is instantiated by the multiplication of matrices, winograd_step A B should be the product of A and ...
Geometrical Probability and Random Points on a Hypersphere.
... and their dual cones generated by points randomly distributed on the surface of a d-sphere. For radially symmetric distributions on the points, the expected nGmber of k-faces and natural measure of the set of k-faces will be found. The expected number of vertices, or extreme points, of convex hulls ...
... and their dual cones generated by points randomly distributed on the surface of a d-sphere. For radially symmetric distributions on the points, the expected nGmber of k-faces and natural measure of the set of k-faces will be found. The expected number of vertices, or extreme points, of convex hulls ...
Polar Decomposition of a Matrix
... because A A is a normal matrix). This means that A∗ Axi = P xi = λi xi where 1 ≤ i ≤ n. It is important to note that λ1 , λ2 , ..., λr > 0 and that λr+1 , λr+2 , ..., λn = 0 because there is the possibility that we do not have a matrix with full rank. To demonstrate this fact we grab the orthonormal ...
... because A A is a normal matrix). This means that A∗ Axi = P xi = λi xi where 1 ≤ i ≤ n. It is important to note that λ1 , λ2 , ..., λr > 0 and that λr+1 , λr+2 , ..., λn = 0 because there is the possibility that we do not have a matrix with full rank. To demonstrate this fact we grab the orthonormal ...
Inverses
... Let A be an n × n matrix. We say that A is invertible (or non-singular) if there is another n × n matrix B such that AB = In = BA . If no such matrix B exists, then matrix A is called non-invertible or singular. If such an n × n matrix B does exist, then B is called “ A inverse” and is then ...
... Let A be an n × n matrix. We say that A is invertible (or non-singular) if there is another n × n matrix B such that AB = In = BA . If no such matrix B exists, then matrix A is called non-invertible or singular. If such an n × n matrix B does exist, then B is called “ A inverse” and is then ...
S.M. Rump. On P-Matrices. Linear Algebra and its Applications
... Proof. Part (i). If the Hermitian part of a matrix C is positive definite, then C has no nonpositive eigenvalues (follows by [13, Theorem 1] or by a field of values argument). Thus A is well defined. For 2(C + C T ) = (C + I)(C T + I) − (C − I)(C T − I) being positive definite, so is I − (C + I)−1 ( ...
... Proof. Part (i). If the Hermitian part of a matrix C is positive definite, then C has no nonpositive eigenvalues (follows by [13, Theorem 1] or by a field of values argument). Thus A is well defined. For 2(C + C T ) = (C + I)(C T + I) − (C − I)(C T − I) being positive definite, so is I − (C + I)−1 ( ...
![arXiv:math/0005256v2 [math.QA] 21 Jun 2000](http://s1.studyres.com/store/data/017029559_1-d28b6a03fef36ff14eaa2fb575ab89be-300x300.png)
arXiv:math/0005256v2 [math.QA] 21 Jun 2000
... for ω ∈ C n (A, M) and xi ∈ A. The cohomology H(A, M) of this cosimplicial module is the M-valued Hochschild cohomology of A. In his case the simplicial differential is called the Hochschild differential. There is a relation between the cohomology of a Lie algebra g and the Hochschild cohomology of ...
... for ω ∈ C n (A, M) and xi ∈ A. The cohomology H(A, M) of this cosimplicial module is the M-valued Hochschild cohomology of A. In his case the simplicial differential is called the Hochschild differential. There is a relation between the cohomology of a Lie algebra g and the Hochschild cohomology of ...
The decompositional approach to matrix computation
... In 1954, Givens showed how to reduce a syn- used primarily to solve positive definite lincar metric matrix A to tridiagonal form by orthogo- systems, as in Equations 3 and 6. It can also be nal transformation.'6 T h e reduction was merely employed to compute quantities usefiil in statisa way station ...
... In 1954, Givens showed how to reduce a syn- used primarily to solve positive definite lincar metric matrix A to tridiagonal form by orthogo- systems, as in Equations 3 and 6. It can also be nal transformation.'6 T h e reduction was merely employed to compute quantities usefiil in statisa way station ...