Chapter 5 Compactness
... a) Any open cover O of X∞ must have a member U containing ∞. Since the complement X∞ \ U is compact, it has a finite subcover {Oi }ni=1 derived from O. Thus, U, O1 , . . . , On is a finite subcover of X∞ . b) The fact that (X, T ) is the subspace topology in (X∞ , T∞ ) basically follows from the def ...
... a) Any open cover O of X∞ must have a member U containing ∞. Since the complement X∞ \ U is compact, it has a finite subcover {Oi }ni=1 derived from O. Thus, U, O1 , . . . , On is a finite subcover of X∞ . b) The fact that (X, T ) is the subspace topology in (X∞ , T∞ ) basically follows from the def ...
Math 490 Extra Handout on the product topology and the box
... for all t ∈ R. Prove that f is not continuous if we give RN the box topology. Notice that this implies that the result of the previous exercise fails for the box topology. 7. Show that RN is disconnected in the box topology. (Hint: Consider the set A of bounded N-tuples and its complement.) So, a pr ...
... for all t ∈ R. Prove that f is not continuous if we give RN the box topology. Notice that this implies that the result of the previous exercise fails for the box topology. 7. Show that RN is disconnected in the box topology. (Hint: Consider the set A of bounded N-tuples and its complement.) So, a pr ...
V.3 Quotient Space
... Suppose we have a function p : X → Y from a topological space X onto a set Y . we want to give a topology on Y so that p becomes a continuous map. Remark If we assign the indiscrete topology on Y , any function p : X → Y would be continuous. But such a topology is too trivial to be useful and the mo ...
... Suppose we have a function p : X → Y from a topological space X onto a set Y . we want to give a topology on Y so that p becomes a continuous map. Remark If we assign the indiscrete topology on Y , any function p : X → Y would be continuous. But such a topology is too trivial to be useful and the mo ...
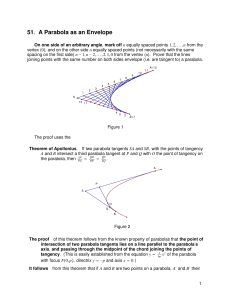
51. A Parabola as an Envelope
... unique such parabola exists.) The tangent line joining the point P numbered 7 on SA SP BQ meets the other side in a point Q so that PA by Apollonius’ Theorem. But QS SP v n"v , and it follows that Q is the point onf SB numbered 7. Thus all the lines PA R drawn connecting like numbered points are ...
... unique such parabola exists.) The tangent line joining the point P numbered 7 on SA SP BQ meets the other side in a point Q so that PA by Apollonius’ Theorem. But QS SP v n"v , and it follows that Q is the point onf SB numbered 7. Thus all the lines PA R drawn connecting like numbered points are ...
3-manifold

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. Intuitively, a 3-manifold can be thought of as a possible shape of the universe. Just like a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.