Fast sparse matrix multiplication ∗
... In this paper we show that the sophisticated algebraic techniques used by the fast matrix multiplication algorithms can nevertheless be used to speed-up the computation of the product of even extremely sparse matrices. More specifically, we present a new algorithm that multiplies two n × n matrices, ...
... In this paper we show that the sophisticated algebraic techniques used by the fast matrix multiplication algorithms can nevertheless be used to speed-up the computation of the product of even extremely sparse matrices. More specifically, we present a new algorithm that multiplies two n × n matrices, ...
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA 1. Lines in
... equations of a pair of lines that illustrate each type of intersection. (2) On one page graph all of the the lines below. Then for each pair in the list eliminate a variable to determine if the pair define the same line, are parallel or intersect at one point. If a pair intersects at one point, find t ...
... equations of a pair of lines that illustrate each type of intersection. (2) On one page graph all of the the lines below. Then for each pair in the list eliminate a variable to determine if the pair define the same line, are parallel or intersect at one point. If a pair intersects at one point, find t ...
The Coding Theory Workbook
... then X is a subset of Y and we would express this relationship as X ⊆ Y . X is said to be a proper subset of Y if |X| < |Y |, and we indicate this by X ⊂ Y . Note that any set X is a subset of itself but not a proper subset of itself, therefore we can write X ⊆ X but we cannot write X ⊂ X. We are of ...
... then X is a subset of Y and we would express this relationship as X ⊆ Y . X is said to be a proper subset of Y if |X| < |Y |, and we indicate this by X ⊂ Y . Note that any set X is a subset of itself but not a proper subset of itself, therefore we can write X ⊆ X but we cannot write X ⊂ X. We are of ...
Eigentheory of Cayley-Dickson algebras
... Cn . Then Eigλ (a) = Eigλ (βa) for any λ. In particular, the eigenvalues of a and βa are the same. See also [MG, Cor. 3.6] for a related result in different notation. Proof. We may assume that a and β both have norm 1. Proposition 3.10 implies that the result holds for all a if it holds for a in C⊥ ...
... Cn . Then Eigλ (a) = Eigλ (βa) for any λ. In particular, the eigenvalues of a and βa are the same. See also [MG, Cor. 3.6] for a related result in different notation. Proof. We may assume that a and β both have norm 1. Proposition 3.10 implies that the result holds for all a if it holds for a in C⊥ ...
Finding a low-rank basis in a matrix subspace
... certificates. An alternative, less cheap, but exact method uses simultaneous diagonalization, which are applicable when d ≤ min(m, n). Applying these methods will often be successful when a rank-one basis exists, but fails if not. This tensor approach seems to have been overseen in the discrete opti ...
... certificates. An alternative, less cheap, but exact method uses simultaneous diagonalization, which are applicable when d ≤ min(m, n). Applying these methods will often be successful when a rank-one basis exists, but fails if not. This tensor approach seems to have been overseen in the discrete opti ...
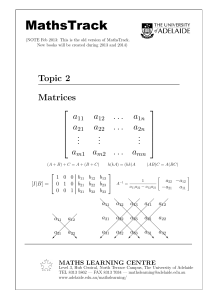
Matrices - The University of Adelaide
... Matrices1 were originally introduced as an aid to solving simultaneous linear equations, but now have an important role in many areas of pure and applied mathematics. Today, matrix theory is used in business, economics, statistics, engineering, operations research, biology, chemistry, physics, meter ...
... Matrices1 were originally introduced as an aid to solving simultaneous linear equations, but now have an important role in many areas of pure and applied mathematics. Today, matrix theory is used in business, economics, statistics, engineering, operations research, biology, chemistry, physics, meter ...
Lecture notes for Linear Algebra
... vM +1 is a nontrivial linear combination of {w1 , w2 , w3 , · · · , wM }, which is a contradiction. 2 The above argument also can be used in the infinite dimensional case, and one can conclude that if there exists one basis that is infinite, then every basis is infinite. It also follows from the pre ...
... vM +1 is a nontrivial linear combination of {w1 , w2 , w3 , · · · , wM }, which is a contradiction. 2 The above argument also can be used in the infinite dimensional case, and one can conclude that if there exists one basis that is infinite, then every basis is infinite. It also follows from the pre ...
Notes on Vector Spaces
... 2. If F n , the set of n-tuples (x1 , x2 , ..., xn ) with x1 = 0 is a subspace; however, the set of n-tuples with x1 = 1 + x2 is not a subspace (n ≥ 2) (why?). 3. The space of polynomial functions over a field F is a subspace of the space of all functions from F into F . 4. The set of all symmetric ...
... 2. If F n , the set of n-tuples (x1 , x2 , ..., xn ) with x1 = 0 is a subspace; however, the set of n-tuples with x1 = 1 + x2 is not a subspace (n ≥ 2) (why?). 3. The space of polynomial functions over a field F is a subspace of the space of all functions from F into F . 4. The set of all symmetric ...
Jordan normal form
In linear algebra, a Jordan normal form (often called Jordan canonical form)of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called a Jordan matrix, representing the operator with respect to some basis. Such matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal (on the superdiagonal), and with identical diagonal entries to the left and below them. If the vector space is over a field K, then a basis with respect to which the matrix has the required form exists if and only if all eigenvalues of the matrix lie in K, or equivalently if the characteristic polynomial of the operator splits into linear factors over K. This condition is always satisfied if K is the field of complex numbers. The diagonal entries of the normal form are the eigenvalues of the operator, with the number of times each one occurs being given by its algebraic multiplicity.If the operator is originally given by a square matrix M, then its Jordan normal form is also called the Jordan normal form of M. Any square matrix has a Jordan normal form if the field of coefficients is extended to one containing all the eigenvalues of the matrix. In spite of its name, the normal form for a given M is not entirely unique, as it is a block diagonal matrix formed of Jordan blocks, the order of which is not fixed; it is conventional to group blocks for the same eigenvalue together, but no ordering is imposed among the eigenvalues, nor among the blocks for a given eigenvalue, although the latter could for instance be ordered by weakly decreasing size.The Jordan–Chevalley decomposition is particularly simple with respect to a basis for which the operator takes its Jordan normal form. The diagonal form for diagonalizable matrices, for instance normal matrices, is a special case of the Jordan normal form.The Jordan normal form is named after Camille Jordan.