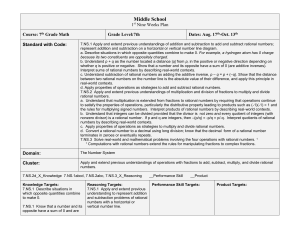
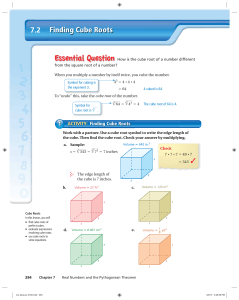
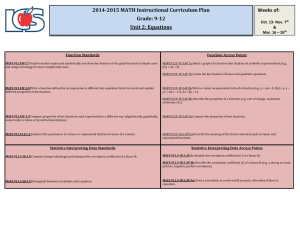
Precalculus: A Prelude to Calculus 1st Edition Paper
... Let’s assume that we have a book that gives the logarithms of the numbers from 1 to 10 in increments of 0.001, meaning that the book gives the logarithms of 1.001, 1.002, 1.003, and so on. The idea is first to compute the right side of the equation above. To do that, we would look in the book of loga ...
... Let’s assume that we have a book that gives the logarithms of the numbers from 1 to 10 in increments of 0.001, meaning that the book gives the logarithms of 1.001, 1.002, 1.003, and so on. The idea is first to compute the right side of the equation above. To do that, we would look in the book of loga ...
An Introduction to Algebraic Number Theory, and the Class Number
... We describe various algebraic invariants of number fields, as well as their applications. These applications relate to prime ramification, the finiteness of the class number, cyclotomic extensions, and the unit theorem. Finally, we present an exposition of the class number formula, which generalizes ...
... We describe various algebraic invariants of number fields, as well as their applications. These applications relate to prime ramification, the finiteness of the class number, cyclotomic extensions, and the unit theorem. Finally, we present an exposition of the class number formula, which generalizes ...
On -adic Saito-Kurokawa lifting and its application
... My adisor Eric Urban deserves many thanks for a lot of things. Not only did he help me pick an interesting problem, without his very helpful guidance and patience throughout the whole process, this thesis is far from what it is today. I would also take this chance to thank Shou-Wu Zhang and Dorian G ...
... My adisor Eric Urban deserves many thanks for a lot of things. Not only did he help me pick an interesting problem, without his very helpful guidance and patience throughout the whole process, this thesis is far from what it is today. I would also take this chance to thank Shou-Wu Zhang and Dorian G ...
GROUP-THEORETIC AND TOPOLOGICAL INVARIANTS OF
... commutative ring theory, such as the ring of integer-valued polynomials [9, Proposition VI.2.1, p. 129], the ring of entire functions [14, Proposition 8.1.1(6), p. 276], the real holomorphy ring of a function field [39, Corollary 3.6], and the Kronecker function ring of a field extension of at most ...
... commutative ring theory, such as the ring of integer-valued polynomials [9, Proposition VI.2.1, p. 129], the ring of entire functions [14, Proposition 8.1.1(6), p. 276], the real holomorphy ring of a function field [39, Corollary 3.6], and the Kronecker function ring of a field extension of at most ...
(IN)CONSISTENCY: SOME LOW-DIMENSIONAL
... takes all values in the interval [0, 1/4] and thus does not satisfy the assumption of Proposition 2. We will return to this example below (Example 3). On the other hand, the conversion method QW described in [3] always gives polynomials Pi of minimal degree, which for Boolean constants are necessari ...
... takes all values in the interval [0, 1/4] and thus does not satisfy the assumption of Proposition 2. We will return to this example below (Example 3). On the other hand, the conversion method QW described in [3] always gives polynomials Pi of minimal degree, which for Boolean constants are necessari ...
A Compact Representation for Modular Semilattices and its
... every median semilattice is compactly represented by, or more specifically, is isomorphic to the family of special ideals of a poset with an additional relation, called an inconsistency relation. This structure is called a poset with inconsistent pairs (PIP), which was also independently introduced ...
... every median semilattice is compactly represented by, or more specifically, is isomorphic to the family of special ideals of a poset with an additional relation, called an inconsistency relation. This structure is called a poset with inconsistent pairs (PIP), which was also independently introduced ...
CLUSTER ALGEBRAS II: FINITE TYPE CLASSIFICATION
... In order to understand a cluster algebra of finite type, one needs to study the combinatorial structure behind it, which is captured by its cluster complex. Roughly speaking, it is defined as follows. The cluster variables for a given cluster algebra are not given from the outset but are obtained fr ...
... In order to understand a cluster algebra of finite type, one needs to study the combinatorial structure behind it, which is captured by its cluster complex. Roughly speaking, it is defined as follows. The cluster variables for a given cluster algebra are not given from the outset but are obtained fr ...