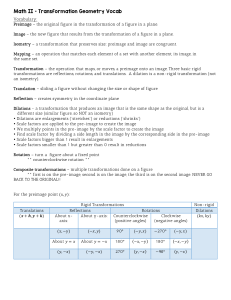
Geometry Unit 2 Worksheet 2
... If two angles share a common vertex, then they are adjacent Which of the following serves as a counterexample to the assertion above? a. ...
... If two angles share a common vertex, then they are adjacent Which of the following serves as a counterexample to the assertion above? a. ...
Semester 1 Outline - Ms-Schmitz-Geometry
... Know alternate interior, alternate exterior, consecutive interior, and corresponding angles and their relationship when lines are parallel( 1 postulate and 3 theorems) slope formula Know how to find equations of lines with slope and a point or two points Know slope intercept form and point slope for ...
... Know alternate interior, alternate exterior, consecutive interior, and corresponding angles and their relationship when lines are parallel( 1 postulate and 3 theorems) slope formula Know how to find equations of lines with slope and a point or two points Know slope intercept form and point slope for ...
02 Spherical Geometry Basics
... • In both, you have angles beween lines. However, in plane geometry, lines that meet do so exactly ones. In spherical, they do so twice, at antipodal points. • There are no parallel lines in spherical geometry! Let’s try looking at triangles. Any three non-collinear points determine a triangle in bo ...
... • In both, you have angles beween lines. However, in plane geometry, lines that meet do so exactly ones. In spherical, they do so twice, at antipodal points. • There are no parallel lines in spherical geometry! Let’s try looking at triangles. Any three non-collinear points determine a triangle in bo ...
Honors Geometry Chapter 7 Review Name
... 17) Are the polygons similar? If so, 1st state the similarity statement and 2nd give the similarity ratio of left polygon to right polygon. A M ...
... 17) Are the polygons similar? If so, 1st state the similarity statement and 2nd give the similarity ratio of left polygon to right polygon. A M ...
Beverley Taylor Sorenson College of Education and Human
... parallelogram and the interior angles between two parallel sides in a trapezoid. The definition of a (regular) polygon and attributes of polygons including the sum of the angles of a polygon and the sum of exterior angles of a polygon. Definitions and Axiomatic Nature of Geometry ...
... parallelogram and the interior angles between two parallel sides in a trapezoid. The definition of a (regular) polygon and attributes of polygons including the sum of the angles of a polygon and the sum of exterior angles of a polygon. Definitions and Axiomatic Nature of Geometry ...
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required. They can be given in several ways, Euler angles being one of them; see charts on SO(3) for others. Euler angles are also used to describe the orientation of a frame of reference (typically, a coordinate system or basis) relative to another. They are typically denoted as α, β, γ, or φ, θ, ψ.Euler angles represent a sequence of three elemental rotations, i.e. rotations about the axes of a coordinate system. For instance, a first rotation about z by an angle α, a second rotation about x by an angle β, and a last rotation again about z, by an angle γ. These rotations start from a known standard orientation. In physics, this standard initial orientation is typically represented by a motionless (fixed, global, or world) coordinate system; in linear algebra, by a standard basis.Any orientation can be achieved by composing three elemental rotations. The elemental rotations can either occur about the axes of the fixed coordinate system (extrinsic rotations) or about the axes of a rotating coordinate system, which is initially aligned with the fixed one, and modifies its orientation after each elemental rotation (intrinsic rotations). The rotating coordinate system may be imagined to be rigidly attached to a rigid body. In this case, it is sometimes called a local coordinate system. Without considering the possibility of using two different conventions for the definition of the rotation axes (intrinsic or extrinsic), there exist twelve possible sequences of rotation axes, divided in two groups: Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y) Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z). Tait–Bryan angles are also called Cardan angles; nautical angles; heading, elevation, and bank; or yaw, pitch, and roll. Sometimes, both kinds of sequences are called ""Euler angles"". In that case, the sequences of the first group are called proper or classic Euler angles.