paper
... on undirected complete graphs with capacities that are randomly selected with a distribution that does not depend on node distance. Note that such results, obtained on undirected graphs, may not be illustrative of the behavior of directed graphs. For example, in directed graphs, the gain that networ ...
... on undirected complete graphs with capacities that are randomly selected with a distribution that does not depend on node distance. Note that such results, obtained on undirected graphs, may not be illustrative of the behavior of directed graphs. For example, in directed graphs, the gain that networ ...
Unification for infinite sets of equations between finite terms
... that then (x)τn is not a variable. Distinguish two cases. - (x)τn−1 6≡ x. Since τn and τn−1 coincide on the domain of τn−1 , we have (x)τn ≡ (x)τn−1 6≡ x. Then Property 3 yields that (x)τn is not a variable. - (x)τn−1 ≡ x. Then x is not in the domain of τn−1 . Furthermore, x = t ∈ Fne where t is not ...
... that then (x)τn is not a variable. Distinguish two cases. - (x)τn−1 6≡ x. Since τn and τn−1 coincide on the domain of τn−1 , we have (x)τn ≡ (x)τn−1 6≡ x. Then Property 3 yields that (x)τn is not a variable. - (x)τn−1 ≡ x. Then x is not in the domain of τn−1 . Furthermore, x = t ∈ Fne where t is not ...
Data Abstraction and Problem Solving with JAVA
... // Displays the input line in reversed order by writing the contents of stack // Writing the contents of stack. stack = readAndCorrect() while (!stack.isEmpty()) { newChar = stack.pop() Write newChar } // end while Advance to new line ...
... // Displays the input line in reversed order by writing the contents of stack // Writing the contents of stack. stack = readAndCorrect() while (!stack.isEmpty()) { newChar = stack.pop() Write newChar } // end while Advance to new line ...
Data Integration: The Teenage Years
... area. Instead of the user having to go to several sources that may have relevant postings (and typically, there are 20-30 such sites in large urban areas), the system should find all the postings for the user. The main contribution of the Information Manifold was the way it described the contents of ...
... area. Instead of the user having to go to several sources that may have relevant postings (and typically, there are 20-30 such sites in large urban areas), the system should find all the postings for the user. The main contribution of the Information Manifold was the way it described the contents of ...
ppt - Multimedia at UCC
... The searching problem The searching problem: If a=[a[i], i=0,1,…,n-1] is an array / list with n elements find whether the element X is in the array and find its position. Inputs: a=[a[i], i=0,1,…,n-1] – the list with n elements Output: pos – int How to do it: Step 1. (initialization) pos=-1; Step 2 ...
... The searching problem The searching problem: If a=[a[i], i=0,1,…,n-1] is an array / list with n elements find whether the element X is in the array and find its position. Inputs: a=[a[i], i=0,1,…,n-1] – the list with n elements Output: pos – int How to do it: Step 1. (initialization) pos=-1; Step 2 ...
Using Python as a Calculator
... Intuitively the return value of a function call is decided by both the function itself and the arguments of the call. To illustrate this, consider two more functions. The int function takes one argument and converts it into an integer, while the float function takes one argument and converts it into ...
... Intuitively the return value of a function call is decided by both the function itself and the arguments of the call. To illustrate this, consider two more functions. The int function takes one argument and converts it into an integer, while the float function takes one argument and converts it into ...
Shortest DNA cyclic cover in compressed space Bastien Cazaux, Rodrigo C´
... overlaps between the words allow to save characters. The Shortest Superstring problem is crucial in text compression. Unfortunately, its hardness prevents us from finding, not only an optimal, but even an approximate solution that is arbitrarily near to optimal [5, 1]. Rather than for a single linea ...
... overlaps between the words allow to save characters. The Shortest Superstring problem is crucial in text compression. Unfortunately, its hardness prevents us from finding, not only an optimal, but even an approximate solution that is arbitrarily near to optimal [5, 1]. Rather than for a single linea ...
LNAI 4031 - Model and Algebra for Genetic Information of Data
... Under the environment of complex networks, data is exchanged frequently. In this process, huge amounts of information about the evolution are created. E.g. when data is published, information hiding behind this operation includes the publisher, publishing time, etc. This information has great signif ...
... Under the environment of complex networks, data is exchanged frequently. In this process, huge amounts of information about the evolution are created. E.g. when data is published, information hiding behind this operation includes the publisher, publishing time, etc. This information has great signif ...
+ X(t)
... • Consider a CT-LTI system. Assume the impulse response of the system is h(t)=e^(-at) for all a>0 and t>0 and input x(t)=u(t). Find the output. y (t ) h(t ) x(t ) h(t ) u (t ) ...
... • Consider a CT-LTI system. Assume the impulse response of the system is h(t)=e^(-at) for all a>0 and t>0 and input x(t)=u(t). Find the output. y (t ) h(t ) x(t ) h(t ) u (t ) ...
Grade 3 – 2005 Practice Test – Problem # 36
... A. Apply and justify the use of a variety of problem-solving strategies; e.g., make an organized list, guess and check. B. Use an organized approach and appropriate strategies to solve multi-step problems. C. Interpret results in the context of the problem being solved; e.g., the solution must be a ...
... A. Apply and justify the use of a variety of problem-solving strategies; e.g., make an organized list, guess and check. B. Use an organized approach and appropriate strategies to solve multi-step problems. C. Interpret results in the context of the problem being solved; e.g., the solution must be a ...
Notes
... Interactions are reads from and writes to variables or fields. Reads and writes are very fast Side effects are instantly seen by all parts of a program ...
... Interactions are reads from and writes to variables or fields. Reads and writes are very fast Side effects are instantly seen by all parts of a program ...
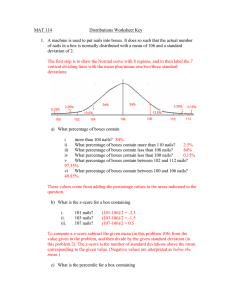
MAT 114 Distributions Worksheet Key 1. A machine is used to put
... d) What is the height of an Ixxian who is at the i. 25th percentile? ...
... d) What is the height of an Ixxian who is at the i. 25th percentile? ...