Department: Physics and Engineering
... B. The development of physical laws, and their expression in the form of mathematical models. C. The application of physical laws in the solution of problems. D. The development of analytical, logical thought processes which are required for problem solution, and which are also applicable in analyzi ...
... B. The development of physical laws, and their expression in the form of mathematical models. C. The application of physical laws in the solution of problems. D. The development of analytical, logical thought processes which are required for problem solution, and which are also applicable in analyzi ...
A MODIFIED TSVD METHOD FOR DISCRETE ILL
... The larger the condition number, the more sensitive can xk be to the error e in b; see, e.g., [13, Lecture 18] for a detailed discussion. The truncation index k is a regularization parameter. It determines how close Ak is to A and how sensitive the computed solution xk is to the error in b. The cond ...
... The larger the condition number, the more sensitive can xk be to the error e in b; see, e.g., [13, Lecture 18] for a detailed discussion. The truncation index k is a regularization parameter. It determines how close Ak is to A and how sensitive the computed solution xk is to the error in b. The cond ...
ODE Lecture Notes, Section 5.3
... Big Idea: The power series solution technique of solving a second-order differential equation is on a firm theoretical footing. That theory gives us insight into the radius of convergence of the solution based on the original differential equation. Big Skill: You should be able to compute the minimu ...
... Big Idea: The power series solution technique of solving a second-order differential equation is on a firm theoretical footing. That theory gives us insight into the radius of convergence of the solution based on the original differential equation. Big Skill: You should be able to compute the minimu ...
CONJUGATE HARMONIC FUNCTIONS IN SEVERAL VARIABLES
... For this purpose we distinguish one of the variables, say xx, and consider the half space E\ of points where xx>0 and (x2,...,xn) are arbitrary. The subspace En_x of points (xt, ...,xn) may be identified with the boundary hyper-plane 0^=0 of Et. Now let f(x2,...,xn) be an arbitrary (say L2) function ...
... For this purpose we distinguish one of the variables, say xx, and consider the half space E\ of points where xx>0 and (x2,...,xn) are arbitrary. The subspace En_x of points (xt, ...,xn) may be identified with the boundary hyper-plane 0^=0 of Et. Now let f(x2,...,xn) be an arbitrary (say L2) function ...
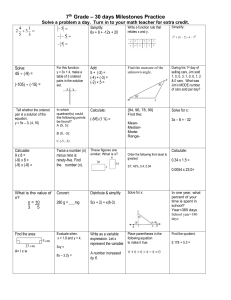
7th Grade – 30 days Milestones Practice Solve a problem a day
... ninety-five. Find the number (n). ...
... ninety-five. Find the number (n). ...