Circles - Blackboard
... When two secant segments are drawn to a circle from an external point, the product of one secant segment and its external segment equals the product of the other secant segment and its external segment. ...
... When two secant segments are drawn to a circle from an external point, the product of one secant segment and its external segment equals the product of the other secant segment and its external segment. ...
1 Triangle ABC is graphed on the set of axes below. Which
... 1) If two lines in a plane are perpendicular to a transversal at different points, then the lines are parallel. 2) If two lines in a plane are cut by a transversal to form congruent corresponding angles, then the lines are parallel. 3) If two lines in a plane are cut by a transversal to form congrue ...
... 1) If two lines in a plane are perpendicular to a transversal at different points, then the lines are parallel. 2) If two lines in a plane are cut by a transversal to form congruent corresponding angles, then the lines are parallel. 3) If two lines in a plane are cut by a transversal to form congrue ...
WATCHMod7Lesson2VideoNotesPart2
... Angles and Parallel Lines When parallel lines get crossed by another line a line called a transversal, several special angles are formed. These angles can be made into pairs of angles which have special names. When lines are parallel alternate interior and corresponding angles are CONGRUENT. Below, ...
... Angles and Parallel Lines When parallel lines get crossed by another line a line called a transversal, several special angles are formed. These angles can be made into pairs of angles which have special names. When lines are parallel alternate interior and corresponding angles are CONGRUENT. Below, ...
Advanced Geometry - Mountain Brook Schools
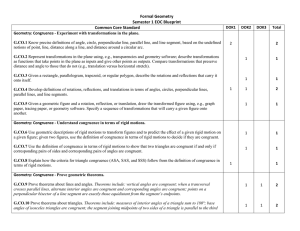
... Experiment with transformations in the plane. 1. Know the precise definitions of angle, circle, perpendicular line, parallel line, and line segment based on the undefined notions of point, line, distance along a line, and distance around a circular arc. (G‐CO1) 2. Represent transformations in the pl ...
... Experiment with transformations in the plane. 1. Know the precise definitions of angle, circle, perpendicular line, parallel line, and line segment based on the undefined notions of point, line, distance along a line, and distance around a circular arc. (G‐CO1) 2. Represent transformations in the pl ...
MAFS.912.G-C.1.2 - Identify and describe relationships among
... This lesson is designed to enable students to develop strategies for describing relationships between right triangles and the radii of their inscribed and circumscribed circles. Students will start this lesson with a win-lose-draw game to review circle vocabulary words. They will then use examples o ...
... This lesson is designed to enable students to develop strategies for describing relationships between right triangles and the radii of their inscribed and circumscribed circles. Students will start this lesson with a win-lose-draw game to review circle vocabulary words. They will then use examples o ...
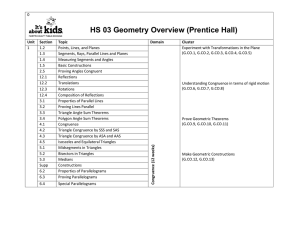
... Line segments in the same plane which do not intersect are parallel Sometimes (when the segments lie on parallel lines) If two lines are cut by a transversal, the rays bisecting a pair of alternate interior angles are parallel. Sometimes – if the two lines cut by the transversal are parallel The opp ...
![PH_Geo_3-8_Constructing_parallel_lines[1]](http://s1.studyres.com/store/data/001202465_1-91ca6e9d9e8948ba2229cefd106376ad-300x300.png)
Riemannian connection on a surface
For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.