Geometric Measure of Aberration in Parabolic Caustics
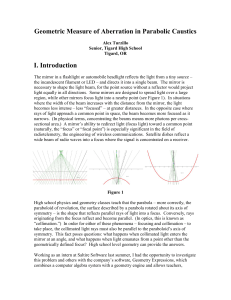
... High school physics and geometry classes teach that the parabola – more correctly, the paraboloid of revolution, the surface described by a parabola rotated about its axis of symmetry – is the shape that reflects parallel rays of light into a focus. Conversely, rays originating from the focus reflec ...
... High school physics and geometry classes teach that the parabola – more correctly, the paraboloid of revolution, the surface described by a parabola rotated about its axis of symmetry – is the shape that reflects parallel rays of light into a focus. Conversely, rays originating from the focus reflec ...
geometry tools - Louisiana Believes
... quickly access and practice on-grade level content. This chart is a reference guide for teachers to help them more quickly identify the specific remedial standards necessary for every geometry math standard6. ...
... quickly access and practice on-grade level content. This chart is a reference guide for teachers to help them more quickly identify the specific remedial standards necessary for every geometry math standard6. ...
7-2 - cloudfront.net
... found by exchanging the hypothesis and conclusion. The converse of a theorem is not automatically true. If it is true, it must be stated as a postulate or proved as a separate theorem. ...
... found by exchanging the hypothesis and conclusion. The converse of a theorem is not automatically true. If it is true, it must be stated as a postulate or proved as a separate theorem. ...
Inscribed Angles, Secant Angles, and Tangent Segments
... Def: A chord of a circle is a line segment that connects two points of the circle. Def: A diameter of a circle is a chord that contains the center. The diameter of a circle is the length of one of these chords. Theorem 56: If a line through the center of a circle is perpendicular to a chord, it ...
... Def: A chord of a circle is a line segment that connects two points of the circle. Def: A diameter of a circle is a chord that contains the center. The diameter of a circle is the length of one of these chords. Theorem 56: If a line through the center of a circle is perpendicular to a chord, it ...
Activity 2 — Properties of Parallel Lines Cut by a Transversal
... Exploring the Basics of Geometry with Cabri ...
... Exploring the Basics of Geometry with Cabri ...
Parallel and Perpendicular Lines
... c. If this growth rate continues when will the median value reach $360,000? 108. The price for the Sunnyside Day Camp to go to the movies is $8 for each adult and $6 for each camper. a. Write an equation that models the information. b. How much will it cost for 4 adults and 15 campers? c. If for eve ...
... c. If this growth rate continues when will the median value reach $360,000? 108. The price for the Sunnyside Day Camp to go to the movies is $8 for each adult and $6 for each camper. a. Write an equation that models the information. b. How much will it cost for 4 adults and 15 campers? c. If for eve ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.