Pre K-Kindergarten Students will be able to: • Sort and classify
... • Use a number line to identify a fractional point. • Compare equivalent fractions using visual representations. • Compare numeric and visual representation of equivalent fractions. • Use models to add/subtract fractions. • Read, name, and write decimals between 0 and 1 up to the hundredths. • Compa ...
... • Use a number line to identify a fractional point. • Compare equivalent fractions using visual representations. • Compare numeric and visual representation of equivalent fractions. • Use models to add/subtract fractions. • Read, name, and write decimals between 0 and 1 up to the hundredths. • Compa ...
Incenter (and Inscribed Circle)
... Circumcenter (and Circumcircle): 1. Click on the triangle symbol and select Polygon. 2. Click to create the first vertex. 3. Move the cursor and click again to create the second vertex. 4. Move the cursor again and click to create the third vertex. 5. Move the cursor back onto the first vertex and c ...
... Circumcenter (and Circumcircle): 1. Click on the triangle symbol and select Polygon. 2. Click to create the first vertex. 3. Move the cursor and click again to create the second vertex. 4. Move the cursor again and click to create the third vertex. 5. Move the cursor back onto the first vertex and c ...
HSCC_Post and Thm PE.indd
... The points on a line can be matched one to one with the real numbers. The real number that corresponds to a point is the coordinate of the point. The distance between points A and B, written as AB, is the absolute value of the difference of the coordinates of A and B. ...
... The points on a line can be matched one to one with the real numbers. The real number that corresponds to a point is the coordinate of the point. The distance between points A and B, written as AB, is the absolute value of the difference of the coordinates of A and B. ...
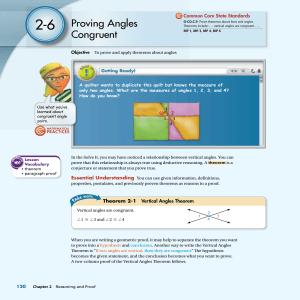
Finding Arc Measures 10.2
... A central angle of a circle is an angle whose vertex is the center of the circle. In the diagram, ∠ACB is a central angle of ⊙C. If m∠ACB is less than 180°, then the points on ⊙C that lie in the interior of ∠ACB form a minor arc with endpoints A and B. The points on ⊙C that do not lie on the minor a ...
... A central angle of a circle is an angle whose vertex is the center of the circle. In the diagram, ∠ACB is a central angle of ⊙C. If m∠ACB is less than 180°, then the points on ⊙C that lie in the interior of ∠ACB form a minor arc with endpoints A and B. The points on ⊙C that do not lie on the minor a ...
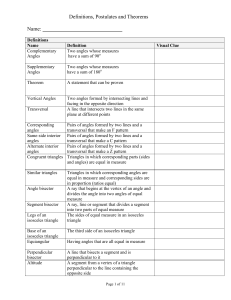
Geometry Definitions, Postulates, and Theorems
... Lines Postulates And Theorems Name Definition Visual Clue Segment Addition For any segment, the measure of the whole postulate is equal to the sum of the measures of its non-overlapping parts Postulate Through any two points there is exactly one line Postulate Common Segments Theorem ...
... Lines Postulates And Theorems Name Definition Visual Clue Segment Addition For any segment, the measure of the whole postulate is equal to the sum of the measures of its non-overlapping parts Postulate Through any two points there is exactly one line Postulate Common Segments Theorem ...
Ab-initio construction of some crystalline 3D Euclidean networks
... mirror lines: these are the intrinsic mirrors lying in the IPMS (often distinct from the extrinsic 3D mirror planes, that are a function of the embedding of the IPMS in E3 )2 . These gridlines give a map of the universal cover of the IPMS in H2 , by the following construction. The symmetries of the ...
... mirror lines: these are the intrinsic mirrors lying in the IPMS (often distinct from the extrinsic 3D mirror planes, that are a function of the embedding of the IPMS in E3 )2 . These gridlines give a map of the universal cover of the IPMS in H2 , by the following construction. The symmetries of the ...
Chapter 4 Notes
... Postulate - ASA – If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. Theorem - AAS – If two angles and a nonincluded side of one triangle are congruent to the corresponding ...
... Postulate - ASA – If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. Theorem - AAS – If two angles and a nonincluded side of one triangle are congruent to the corresponding ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑