Mathematical Origami: PHiZZ Dodecahedron
... Every Platonic solid has a dual polyhedron which is another Platonic solid. The dual is formed by placing a vertex in the center of each face of a Platonic solid. The resulting polyhedron is another Platonic solid. The dual of the octahedron is the cube and vice versa. Similarly the icosahedron and ...
... Every Platonic solid has a dual polyhedron which is another Platonic solid. The dual is formed by placing a vertex in the center of each face of a Platonic solid. The resulting polyhedron is another Platonic solid. The dual of the octahedron is the cube and vice versa. Similarly the icosahedron and ...
Transitional Algebra/Geometry
... Recognize and describe the real number system and use the properties of rational numbers. Use reciprocals in solving equations dealing with rational numbers. Utilize those properties necessary to work with r ...
... Recognize and describe the real number system and use the properties of rational numbers. Use reciprocals in solving equations dealing with rational numbers. Utilize those properties necessary to work with r ...
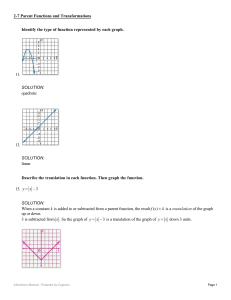
Identify the type of function represented by each graph. 11. SOLUTION
... When a constant k is added to or subtracted from a parent function, the result is a translation of the graph up or down. When a constant h is added to or subtracted from x before evaluating a parent function, the result, , is a translation left or right. The graph is moved 6 units down and 4 units ...
... When a constant k is added to or subtracted from a parent function, the result is a translation of the graph up or down. When a constant h is added to or subtracted from x before evaluating a parent function, the result, , is a translation left or right. The graph is moved 6 units down and 4 units ...
8.4
... Circular cylinder: formed by two parallel planes intersecting a sphere and the line segments connecting the circular regions by their edges such that every perpendicular planar cross section of the cylinder would be a circular region; the bases of the cylinder are circles, while the lateral face of ...
... Circular cylinder: formed by two parallel planes intersecting a sphere and the line segments connecting the circular regions by their edges such that every perpendicular planar cross section of the cylinder would be a circular region; the bases of the cylinder are circles, while the lateral face of ...
CONVEX PARTITIONS OF POLYHEDRA
... genus k. Similarly, polyhedra may have holes (i.e., handles), and we define the genus of a polyhedron as the genus of the surface formed by its boundary [6]. It follows from the definition that a polyhedron may not have interior boundaries. Let P be a polyhedron with n vertices vl," vn, p edges el,. ...
... genus k. Similarly, polyhedra may have holes (i.e., handles), and we define the genus of a polyhedron as the genus of the surface formed by its boundary [6]. It follows from the definition that a polyhedron may not have interior boundaries. Let P be a polyhedron with n vertices vl," vn, p edges el,. ...
Math 1350 Review #1
... 8. A star is formed by extending the sides of a regular pentagon to form five congruent isosceles triangles. What is the sum of the measures of A , B , C , D , and E ? A ...
... 8. A star is formed by extending the sides of a regular pentagon to form five congruent isosceles triangles. What is the sum of the measures of A , B , C , D , and E ? A ...
8.3 - DPS ARE
... a. Which kind of fruit costs more per pound? Explain b. Bananas cost less per pound than peaches or plums. Draw a line alongside the other graphs that might represent the cost y of buying x pounds of bananas. Correct Answer(s) a. Peaches cost more per pound. This can be determined by the steepness o ...
... a. Which kind of fruit costs more per pound? Explain b. Bananas cost less per pound than peaches or plums. Draw a line alongside the other graphs that might represent the cost y of buying x pounds of bananas. Correct Answer(s) a. Peaches cost more per pound. This can be determined by the steepness o ...
Problems 93 - Abelkonkurransen
... least number of vertices one must remove from this set, so that no 4 points of the remaining set are the vertices of any square with sides parallel to the sides of the initial square? 15. On each face of two dice some positive integer is written. The two dice are thrown and the numbers on the top fa ...
... least number of vertices one must remove from this set, so that no 4 points of the remaining set are the vertices of any square with sides parallel to the sides of the initial square? 15. On each face of two dice some positive integer is written. The two dice are thrown and the numbers on the top fa ...
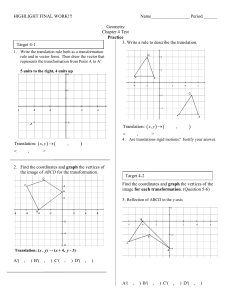
Geometry Chapter 4 Test Practice 2. Find the coordinates an
... rule and in vector form. Then draw the vector that represents the transformation from Point A to A’. 5 units to the right, 4 units up ...
... rule and in vector form. Then draw the vector that represents the transformation from Point A to A’. 5 units to the right, 4 units up ...
f.i-*2y:5
... lines whose equatiorts 25. GEOMETRY The sides of an angle are parts of two vertex is the point where the 2y + 3x: - i*:g]rhe angle's the angle. two sides meet. Finh the coordinater of the vertex of ...
... lines whose equatiorts 25. GEOMETRY The sides of an angle are parts of two vertex is the point where the 2y + 3x: - i*:g]rhe angle's the angle. two sides meet. Finh the coordinater of the vertex of ...
PretestReview_9_2_15
... all variables on the same side of the = sign. Step 4: Isolate the variable term by subtracting (-) or adding (+) the constant (number with no variable) from each side of the equation. Step 5: Isolate the variable by dividing both sides of the equation by the coefficient of the ...
... all variables on the same side of the = sign. Step 4: Isolate the variable term by subtracting (-) or adding (+) the constant (number with no variable) from each side of the equation. Step 5: Isolate the variable by dividing both sides of the equation by the coefficient of the ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑