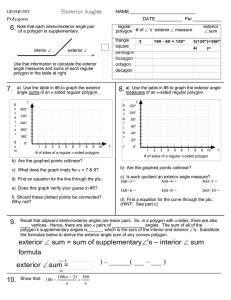
6. 8. exterior ∠ sum = sum of supplementary∠`s – interior ∠ sum
... Recall that adjacent interior/exterior angles are linear pairs. So, in a polygon with n-sides, there are also ____ vertices. Hence, there are also n pairs of _____________ angles. The sum of all of the polygon’s supplementary angles is______, which is the sum of the interior and exterior ∠’s. Substi ...
... Recall that adjacent interior/exterior angles are linear pairs. So, in a polygon with n-sides, there are also ____ vertices. Hence, there are also n pairs of _____________ angles. The sum of all of the polygon’s supplementary angles is______, which is the sum of the interior and exterior ∠’s. Substi ...
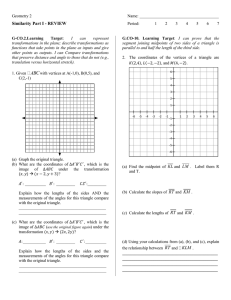
Name
... that are equal distance from the endpoints of a given segment. The definition is the same for Taxicab Geometry; however, a Taxicab perpendicular bisector looks different than a Euclidean perpendicular bisector. Given two points, A ( 1, 1) B (6, 4) graph the Taxicab ...
... that are equal distance from the endpoints of a given segment. The definition is the same for Taxicab Geometry; however, a Taxicab perpendicular bisector looks different than a Euclidean perpendicular bisector. Given two points, A ( 1, 1) B (6, 4) graph the Taxicab ...
Elementary Algebra and Functions The Distributive Property
... Factoring out a GCF Factoring out the GCF in Polynomial Expressions Using the Zero Product Property to Solve Quadratic Equations Solving Quadratic Equations by Factoring Distance/Rate/Time Word Problems Simple Interest Word Problems Using Systems of Equations to Model Age Problems Integer Exponents ...
... Factoring out a GCF Factoring out the GCF in Polynomial Expressions Using the Zero Product Property to Solve Quadratic Equations Solving Quadratic Equations by Factoring Distance/Rate/Time Word Problems Simple Interest Word Problems Using Systems of Equations to Model Age Problems Integer Exponents ...
Platonic Solids
... • Start by making two separate pentagons. One will form the top of the dodecahedron; the other forms the bottom. • One obvious way to connect the two pentagons is with vertical sticks. Why doesn’t that give us a regular polyhedron? [look for squares] • Try building a pentagon using two vertices of t ...
... • Start by making two separate pentagons. One will form the top of the dodecahedron; the other forms the bottom. • One obvious way to connect the two pentagons is with vertical sticks. Why doesn’t that give us a regular polyhedron? [look for squares] • Try building a pentagon using two vertices of t ...
Discrete Volume Polyhedrization is Srongly NP-Hard
... In recent years DVP is attracting an increasing interest, mainly driven by its rich set of applications. A substantial body of literature impossible to report here has been developed on the subject considered from diverse points of view. For instance, a lot of related work is available in any volume ...
... In recent years DVP is attracting an increasing interest, mainly driven by its rich set of applications. A substantial body of literature impossible to report here has been developed on the subject considered from diverse points of view. For instance, a lot of related work is available in any volume ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑