Geom-22 Midterm Review - Fairfield Public Schools
... f) Another way to name a ray with endpoint P ...
... f) Another way to name a ray with endpoint P ...
topic 9 geometry proofs
... When you solve an equation in algebra, you are doing a step-by-step process to convince someone that an answer is valid. That is the process of writing a proof. So we will begin by looking at the steps in the solution of an equation, adding the algebra reasons for each step. These reasons will come ...
... When you solve an equation in algebra, you are doing a step-by-step process to convince someone that an answer is valid. That is the process of writing a proof. So we will begin by looking at the steps in the solution of an equation, adding the algebra reasons for each step. These reasons will come ...
© Sherry Scarborough, Lynnette Cardenas 7/8/2005 ... polygon is the sum of the lengths of the sides... Math 366 Study Guide (revised with thanks to Lynnette Cardenas)
... Identify pyramids and their parts (base, apex, lateral faces). Identify convex and concave polyhedra. Identify the characteristics of a regular polyhedron. Identify the five regular polyhedra by name, their number of faces, and the shape of their faces. (See Table 9-10, p. 539.) Define a net. Recogn ...
... Identify pyramids and their parts (base, apex, lateral faces). Identify convex and concave polyhedra. Identify the characteristics of a regular polyhedron. Identify the five regular polyhedra by name, their number of faces, and the shape of their faces. (See Table 9-10, p. 539.) Define a net. Recogn ...
Polygons 7.1 Triangle Application Theorems
... two triangles such that two ______and a ___________side of one are congruent to the corresponding parts of the other, then the triangles are congruent. ( AAS) Given: ∠ G ≅ ∠ K ∠ H ≅ ∠ M Prove: Δ GHJ ≅ Δ KMO ...
... two triangles such that two ______and a ___________side of one are congruent to the corresponding parts of the other, then the triangles are congruent. ( AAS) Given: ∠ G ≅ ∠ K ∠ H ≅ ∠ M Prove: Δ GHJ ≅ Δ KMO ...
Scott - Modifying Minkowski`s theorem
... At the turn of the century, Minkowski published his famous “convex body” theorem which became the basis for the geometry of numbers. Suppose that A is a lattice in Euclidean n-space, E”, having determinant d(A). Now Minkowski’s theorem states that if K is a convex body which is symmetric about the o ...
... At the turn of the century, Minkowski published his famous “convex body” theorem which became the basis for the geometry of numbers. Suppose that A is a lattice in Euclidean n-space, E”, having determinant d(A). Now Minkowski’s theorem states that if K is a convex body which is symmetric about the o ...
Study Guide for the Midterm Exam
... Definitions, notions and axioms to remember 1. Axioms: Euclid’s postulates (I may ask you also about Birkhoff’s and Hilbert’s axioms, or to use the SMSG postulates, but if I do so, I will provide a copy of those), Playfair’s postulate (page 48), Elliptic Parallel Postulate (page 78). 2. Definitions ...
... Definitions, notions and axioms to remember 1. Axioms: Euclid’s postulates (I may ask you also about Birkhoff’s and Hilbert’s axioms, or to use the SMSG postulates, but if I do so, I will provide a copy of those), Playfair’s postulate (page 48), Elliptic Parallel Postulate (page 78). 2. Definitions ...
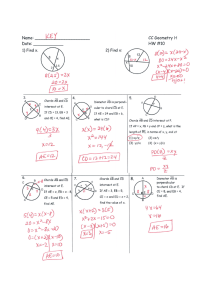
Geometry 1-6 9-2
... Mathematical Practices 2 Reason abstractly and quantitatively. 6 Attend to precision. ...
... Mathematical Practices 2 Reason abstractly and quantitatively. 6 Attend to precision. ...
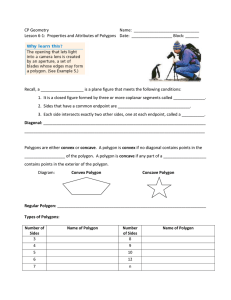
Geometry22 Name: Per: ______ Date: ______ 3
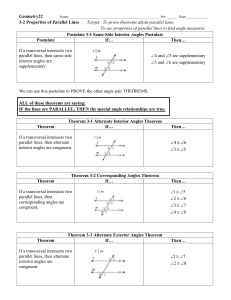
... ALL of these theorems are saying: IF the lines are PARALLEL, THEN the special angle relationships are true. ...
... ALL of these theorems are saying: IF the lines are PARALLEL, THEN the special angle relationships are true. ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑