Parallel and Perpendicular Lines
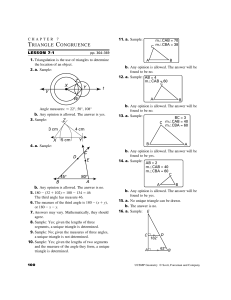
... different angle. Add a row 2nd Measure to your table and record the new measures. Repeat these steps until your table has 3rd, 4th, and 5th Measure rows of data. 3. Using the angles listed in the table, identify and describe the relationship between all angle pairs that have the following special na ...
... different angle. Add a row 2nd Measure to your table and record the new measures. Repeat these steps until your table has 3rd, 4th, and 5th Measure rows of data. 3. Using the angles listed in the table, identify and describe the relationship between all angle pairs that have the following special na ...
Lesson 2.3 Powerpoint - peacock
... • Why did the geometry student get so excited after they finished a jigsaw puzzle ...
... • Why did the geometry student get so excited after they finished a jigsaw puzzle ...
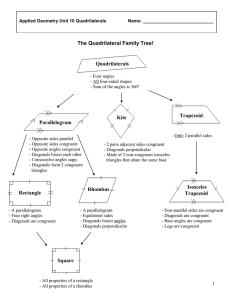
Polygons and Quadrilaterals
... 1. Plot the points A(2, 2), B(4, −2),C(−2, −4), and D(−6, −2). a. Find the slopes of AB, BC,CD, and AD. Is ABCD a parallelogram? b. Find the point of intersection of the diagonals by finding the midpoint of each. Know What? You are marking out a baseball diamond and standing at home plate. 3rd base ...
... 1. Plot the points A(2, 2), B(4, −2),C(−2, −4), and D(−6, −2). a. Find the slopes of AB, BC,CD, and AD. Is ABCD a parallelogram? b. Find the point of intersection of the diagonals by finding the midpoint of each. Know What? You are marking out a baseball diamond and standing at home plate. 3rd base ...
Spherical f-tilings by two non congruent classes of isosceles
... Abstract. The theory of f-tilings is related to the theory of isometric foldings, initiated by S. Robertson [8] in 1977. The study of dihedral f-tilings of the Euclidean sphere S 2 by triangles and r-sided regular polygons was initiated in 2004, where the case r = 4 was considered [4]. In a subseque ...
... Abstract. The theory of f-tilings is related to the theory of isometric foldings, initiated by S. Robertson [8] in 1977. The study of dihedral f-tilings of the Euclidean sphere S 2 by triangles and r-sided regular polygons was initiated in 2004, where the case r = 4 was considered [4]. In a subseque ...
Chapter 6 Polygons and Quadrilaterals
... Standard G-4: The student will demonstrate an understanding of quadrilaterals and other polygons, their properties, and relationships between or among them. ...
... Standard G-4: The student will demonstrate an understanding of quadrilaterals and other polygons, their properties, and relationships between or among them. ...
The A to Z of Mathematics - Pendidikan Matematika USN
... Throughout the world many people suffer from the same problem: math anxiety. No other area of skill seems to polarize people so readily into two contrasting groups, those who can do math and those who cannot. Of the two groups, the second one is by far the larger. To succeed in mathematics you need ...
... Throughout the world many people suffer from the same problem: math anxiety. No other area of skill seems to polarize people so readily into two contrasting groups, those who can do math and those who cannot. Of the two groups, the second one is by far the larger. To succeed in mathematics you need ...
The A to Z of Mathematics
... Throughout the world many people suffer from the same problem: math anxiety. No other area of skill seems to polarize people so readily into two contrasting groups, those who can do math and those who cannot. Of the two groups, the second one is by far the larger. To succeed in mathematics you need ...
... Throughout the world many people suffer from the same problem: math anxiety. No other area of skill seems to polarize people so readily into two contrasting groups, those who can do math and those who cannot. Of the two groups, the second one is by far the larger. To succeed in mathematics you need ...
CK-12 Geometry: Proving Quadrilaterals are Parallelograms
... Example 1 proves an additional way to show that a quadrilateral is a parallelogram. Theorem 5-10: If a quadrilateral has one set of parallel lines that are also congruent, then it is a parallelogram. Example 2: Is quadrilateral a parallelogram? How do you know? ...
... Example 1 proves an additional way to show that a quadrilateral is a parallelogram. Theorem 5-10: If a quadrilateral has one set of parallel lines that are also congruent, then it is a parallelogram. Example 2: Is quadrilateral a parallelogram? How do you know? ...
What is a Parallelogram?
... b. Rotate the ruler and repeat this so that you have a parallelogram. Your second set of parallel lines can be any length. If you have colored pencils, outline the ...
... b. Rotate the ruler and repeat this so that you have a parallelogram. Your second set of parallel lines can be any length. If you have colored pencils, outline the ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑