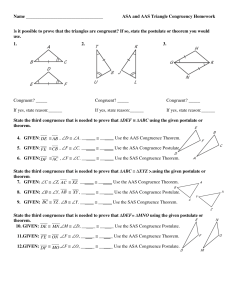
ASA and AAS Triangle Congruency Homework Is it possible
... State the third congruence that is needed to prove that ∆DEF ≅ ∆ABC using the given postulate or theorem. 4. GIVEN: DE ≅ AB , ∠D ≅ ∠A. ______ ≅ ______ Use the AAS Congruence Theorem. 5. GIVEN: FE ≅ CB , ∠F ≅ ∠C. ______ ≅ ______ Use the ASA Congruence Postulate. 6. GIVEN: DF ≅ AC , ∠F ≅ ∠C. ______ ≅ ...
... State the third congruence that is needed to prove that ∆DEF ≅ ∆ABC using the given postulate or theorem. 4. GIVEN: DE ≅ AB , ∠D ≅ ∠A. ______ ≅ ______ Use the AAS Congruence Theorem. 5. GIVEN: FE ≅ CB , ∠F ≅ ∠C. ______ ≅ ______ Use the ASA Congruence Postulate. 6. GIVEN: DF ≅ AC , ∠F ≅ ∠C. ______ ≅ ...
Geometry: Unit 3 Review
... of concurrence of the three internal of concurrence of the three angle bisectors. The radius of the altitudes. The radius of the circle is circle is the segment that joins the the segment that joins the center center and one side of the triangle and one of the vertices of the and is perpendicular to ...
... of concurrence of the three internal of concurrence of the three angle bisectors. The radius of the altitudes. The radius of the circle is circle is the segment that joins the the segment that joins the center center and one side of the triangle and one of the vertices of the and is perpendicular to ...
Exemplar 6: Construction and Properties of Polyhedra
... with equilateral triangles, at each vertex of the polyhedra formed, there can only be either 3, 4 or 5 triangles joined together which resulted in tetrahedron, octahedron, and icosahedron respectively. (c) with squares, at each vertex of the polyhedra formed, there can only be 3 squares joining toge ...
... with equilateral triangles, at each vertex of the polyhedra formed, there can only be either 3, 4 or 5 triangles joined together which resulted in tetrahedron, octahedron, and icosahedron respectively. (c) with squares, at each vertex of the polyhedra formed, there can only be 3 squares joining toge ...
Ch. XI Circles
... draw the picture with the information given to me. Second, I will add lines so I can relate this to problems I have solved before, and third I will label the diagram. In this proof, I will be able to construct a triangle by connecting two points, that triangle will have an exterior angle formed (the ...
... draw the picture with the information given to me. Second, I will add lines so I can relate this to problems I have solved before, and third I will label the diagram. In this proof, I will be able to construct a triangle by connecting two points, that triangle will have an exterior angle formed (the ...
Theta Three-Dimensional Geometry 2013 ΜΑΘ
... 21. The ratio between the radii of two spheres is 5:3. What is the ratio of the volume of the larger sphere to the volume of the smaller sphere? (A) 25√2/3 ...
... 21. The ratio between the radii of two spheres is 5:3. What is the ratio of the volume of the larger sphere to the volume of the smaller sphere? (A) 25√2/3 ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑