Methods of Geometry
... solution, and where to look for a strategy. Instructors should welcome questions ; that's what we're here for. The author generally prefers to see several attempts at most exercises, each one more detailed or progressing farther t h a n its predecessor. In the end students will have portfolios of co ...
... solution, and where to look for a strategy. Instructors should welcome questions ; that's what we're here for. The author generally prefers to see several attempts at most exercises, each one more detailed or progressing farther t h a n its predecessor. In the end students will have portfolios of co ...
Topic 6 Polygons and Quadrilaterals
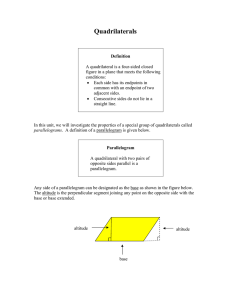
... interior angles of quadrilaterals. Draw several quadrilaterals with parallel opposite sides. Measure the interior angles. b. Make two conjectures about the interior angles of this type of quadrilateral. ...
... interior angles of quadrilaterals. Draw several quadrilaterals with parallel opposite sides. Measure the interior angles. b. Make two conjectures about the interior angles of this type of quadrilateral. ...
Chapter 8: Quadrilaterals
... Example 1 Interior Angles of Regular Polygons CHEMISTRY The benzene molecule, C6H6, consists of six carbon atoms in a regular hexagonal pattern with a hydrogen atom attached to each carbon atom. Find the sum of the measures of the interior angles of the hexagon. Since the molecule is a convex polyg ...
... Example 1 Interior Angles of Regular Polygons CHEMISTRY The benzene molecule, C6H6, consists of six carbon atoms in a regular hexagonal pattern with a hydrogen atom attached to each carbon atom. Find the sum of the measures of the interior angles of the hexagon. Since the molecule is a convex polyg ...
Chapter 8: Quadrilaterals
... Example 1 Interior Angles of Regular Polygons CHEMISTRY The benzene molecule, C6H6, consists of six carbon atoms in a regular hexagonal pattern with a hydrogen atom attached to each carbon atom. Find the sum of the measures of the interior angles of the hexagon. Since the molecule is a convex polyg ...
... Example 1 Interior Angles of Regular Polygons CHEMISTRY The benzene molecule, C6H6, consists of six carbon atoms in a regular hexagonal pattern with a hydrogen atom attached to each carbon atom. Find the sum of the measures of the interior angles of the hexagon. Since the molecule is a convex polyg ...
6.4 Notes
... If an angle of a quadrilateral is supplementary to both consecutive angles, then the quadrilateral is a parallelogram. If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. If one pair of opposite sides of a quadrilateral are both congruent and paral ...
... If an angle of a quadrilateral is supplementary to both consecutive angles, then the quadrilateral is a parallelogram. If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. If one pair of opposite sides of a quadrilateral are both congruent and paral ...
SYMMETRIES OF MONOCORONAL TILINGS 1. Introduction The
... polygons are face-to-face if the intersection of two tiles is either an entire edge of both of the tiles, or a vertex of both of the tiles, or empty. Definition 1.1. Let x be a vertex in some tiling T . The vertex-corona of x is the set of all tiles T ∈ T such that x ∈ T , together with x. In tiling ...
... polygons are face-to-face if the intersection of two tiles is either an entire edge of both of the tiles, or a vertex of both of the tiles, or empty. Definition 1.1. Let x be a vertex in some tiling T . The vertex-corona of x is the set of all tiles T ∈ T such that x ∈ T , together with x. In tiling ...
Reg Geometry Midterm Practice Test
... A plumber knows that if you shut off the water at the main valve, it is safe to remove the sink faucet. The plumber turns the main valve to the “off” position. What conclusion can the plumber make? A It is not safe to remove the sink faucet. B It is safe to remove the sink faucet. C The water is not ...
... A plumber knows that if you shut off the water at the main valve, it is safe to remove the sink faucet. The plumber turns the main valve to the “off” position. What conclusion can the plumber make? A It is not safe to remove the sink faucet. B It is safe to remove the sink faucet. C The water is not ...
Polyhedra and Geodesic Structures
... Happily, it is much easier to construct a τ : 1-decagon – that is, a decagon all of whose angles have measure 144◦ but whose sides alternate in the ratios τ and 1. One simply constructs a regular pentagon, trisects the sides, and “connects the dots” (see Figure 1.6(b)). That this yields a τ : 1-deca ...
... Happily, it is much easier to construct a τ : 1-decagon – that is, a decagon all of whose angles have measure 144◦ but whose sides alternate in the ratios τ and 1. One simply constructs a regular pentagon, trisects the sides, and “connects the dots” (see Figure 1.6(b)). That this yields a τ : 1-deca ...
CHAPTER 1. LINES AND PLANES IN SPACE §1. Angles and
... two intersecting lines in this plane, then (by Problem 1.12) its projection to plane Π is parallel to the bisector of one of the two angles formed by these lines. We may assume that all the three lines meet at one point. If line l is the bisector of the angle between lines l1 and l2 , then l1 and l2 ...
... two intersecting lines in this plane, then (by Problem 1.12) its projection to plane Π is parallel to the bisector of one of the two angles formed by these lines. We may assume that all the three lines meet at one point. If line l is the bisector of the angle between lines l1 and l2 , then l1 and l2 ...
Since P is the centroid of the triangle ACE
... To determine each point of concurrency, you must perform their corresponding constructions. You may want to make a different tracing for each center so your lines and arcs won't get confusing.To determine if the blue peg is a circumcenter, construct the perpendicular bisectors of each side. To deter ...
... To determine each point of concurrency, you must perform their corresponding constructions. You may want to make a different tracing for each center so your lines and arcs won't get confusing.To determine if the blue peg is a circumcenter, construct the perpendicular bisectors of each side. To deter ...
Polygons and Quadrilaterals
... What is the sum of the angles in a 15-gon? What is the sum of the angles in a 23-gon? The sum of the interior angles of a polygon is 4320◦ . How many sides does the polygon have? The sum of the interior angles of a polygon is 3240◦ . How many sides does the polygon have? What is the measure of each ...
... What is the sum of the angles in a 15-gon? What is the sum of the angles in a 23-gon? The sum of the interior angles of a polygon is 4320◦ . How many sides does the polygon have? The sum of the interior angles of a polygon is 3240◦ . How many sides does the polygon have? What is the measure of each ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑