Determine the equation of a line given any of the following
... Given two parallel lines and a transversal, I can identify alternate interior angles, alternate exterior angles, same-side interior angles, and corresponding angles and determine which are equal in measure and which are supplementary. I can write a two column proof that proves two lines are parallel ...
... Given two parallel lines and a transversal, I can identify alternate interior angles, alternate exterior angles, same-side interior angles, and corresponding angles and determine which are equal in measure and which are supplementary. I can write a two column proof that proves two lines are parallel ...
a few inequalities in quadrilaterals
... only if the quadrilateral is cyclic, has perpendicular diagonals and both pairs of opposite sides are congruent. This is equivalent to a square. A right kite is de…ned to be a kite with two opposite right angles (or a cyclic kite, in which case the two opposite right angles is a direct corollary). N ...
... only if the quadrilateral is cyclic, has perpendicular diagonals and both pairs of opposite sides are congruent. This is equivalent to a square. A right kite is de…ned to be a kite with two opposite right angles (or a cyclic kite, in which case the two opposite right angles is a direct corollary). N ...
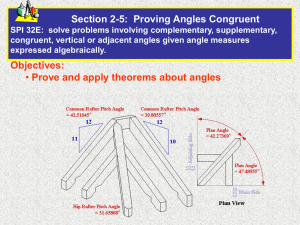
Congruence Theorems in Action
... Unless, however, you’re talking about a spherical triangle. A spherical triangle is a triangle formed on the surface of a sphere. The sum of the measures of the angles of this kind of triangle is always greater than 180°. Spherical triangles can have two or even three obtuse angles or right angles. ...
... Unless, however, you’re talking about a spherical triangle. A spherical triangle is a triangle formed on the surface of a sphere. The sum of the measures of the angles of this kind of triangle is always greater than 180°. Spherical triangles can have two or even three obtuse angles or right angles. ...
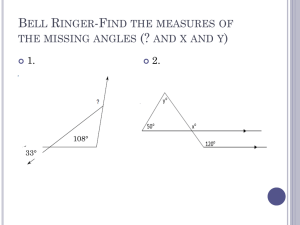
Warm Up - BFHS
... The equation y = 3x + 3 can be used to represent Woodland Avenue. His school lies at the origin. The school bus will pick him up only if he lives farther than 2 miles from the school. If each unit on a coordinate plane represents 1 mile, find the distance from his house to the school to determine if ...
... The equation y = 3x + 3 can be used to represent Woodland Avenue. His school lies at the origin. The school bus will pick him up only if he lives farther than 2 miles from the school. If each unit on a coordinate plane represents 1 mile, find the distance from his house to the school to determine if ...
VDOE ESS Activity Sheet 1: Angles in Polygons
... is the sum of the measures of the interior angles in a convex pentagon? ________ 5. Repeat #4, adding a side until you find patterns for the number of triangles and the sum of the measures of the interior angles. 6. Complete columns #3 and #5 of the table. 7. If the sum of the measures of the interi ...
... is the sum of the measures of the interior angles in a convex pentagon? ________ 5. Repeat #4, adding a side until you find patterns for the number of triangles and the sum of the measures of the interior angles. 6. Complete columns #3 and #5 of the table. 7. If the sum of the measures of the interi ...
Prove
... Corresponding Angles Theorem: If two parallel lines are cut by a transversal, then the pairs of corresponding angles are ____________________________________________. Alternate Interior Angles Theorem: If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are___ ...
... Corresponding Angles Theorem: If two parallel lines are cut by a transversal, then the pairs of corresponding angles are ____________________________________________. Alternate Interior Angles Theorem: If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are___ ...
Ch 4 Notes
... Standards: 5.0 Students prove that triangles are congruent or similar, and they are able to use the concept of corresponding parts of congruent triangles. 12.0 Students find and use measures of sides and of interior and exterior angles of triangles and polygons to classify figures and solve problems ...
... Standards: 5.0 Students prove that triangles are congruent or similar, and they are able to use the concept of corresponding parts of congruent triangles. 12.0 Students find and use measures of sides and of interior and exterior angles of triangles and polygons to classify figures and solve problems ...
9-1 Basic Terms associated with Circles and Spheres
... Theorem 9-12 When two ________ segments are drawn to a circle from an _________ _____________, the product of one secant segment and its __________ ______________ is equal to the product of the other secant segment and its _______________________ That is, in the circle below, ...
... Theorem 9-12 When two ________ segments are drawn to a circle from an _________ _____________, the product of one secant segment and its __________ ______________ is equal to the product of the other secant segment and its _______________________ That is, in the circle below, ...
Chapter 10 - Properties of Circles
... 10.1 – Use Properties of Tangents • Circle • Set of all points in a plan that are equidistant from a given point called center of circle • Radius • Segment whose endpoints are center and any point on circle • Chord • Segment whose endpoints are on circle • Diameter • Chord that contains center of c ...
... 10.1 – Use Properties of Tangents • Circle • Set of all points in a plan that are equidistant from a given point called center of circle • Radius • Segment whose endpoints are center and any point on circle • Chord • Segment whose endpoints are on circle • Diameter • Chord that contains center of c ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑