1 Lecture 7 THE POINCARÉ DISK MODEL OF HYPERBOLIC
... 7.8. Hyperbolic geometry and the physical world In his famous book Science et Hypothèse, Henri Poincaré describes the physics of a small “universe” and the physical theories that its inhabitants would create. The universe considered by Poincaré is Euclidean, plane (twodimensional), has the form o ...
... 7.8. Hyperbolic geometry and the physical world In his famous book Science et Hypothèse, Henri Poincaré describes the physics of a small “universe” and the physical theories that its inhabitants would create. The universe considered by Poincaré is Euclidean, plane (twodimensional), has the form o ...
Pre-AP Geometry
... distance around a circular arc (4th nine weeks). Prove geometric theorems G-CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points o ...
... distance around a circular arc (4th nine weeks). Prove geometric theorems G-CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points o ...
ACCRS/QualityCore-Geometry Correlation - UPDATED
... C.1.e Using Logic and Proof to Reason Mathematically; Logic and Proof; Read and write different types and formats of proofs including two-column, flowchart, paragraph, and indirect proofs. C.1.i Using Logic and Proof to Reason Mathematically; Logic and Proof; Use properties of special quadrilateral ...
... C.1.e Using Logic and Proof to Reason Mathematically; Logic and Proof; Read and write different types and formats of proofs including two-column, flowchart, paragraph, and indirect proofs. C.1.i Using Logic and Proof to Reason Mathematically; Logic and Proof; Use properties of special quadrilateral ...
8-3
... Use trigonometric ratios to find angle measures in right triangles and to solve real-world problems. ...
... Use trigonometric ratios to find angle measures in right triangles and to solve real-world problems. ...
2205 Unit 1 NOTES - North Penn School District
... Segment bisector – a point, line, or ray that intersects a segment at its __________________ Label CD and midpoint M to show that MN is the segment bisector of CD . ...
... Segment bisector – a point, line, or ray that intersects a segment at its __________________ Label CD and midpoint M to show that MN is the segment bisector of CD . ...
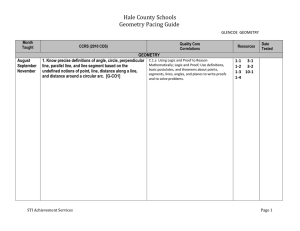
Hale County Schools
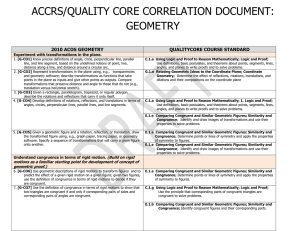
... 1. Know precise definitions of angle, circle, perpendicular C.1.a Using Logic and Proof to Reason Mathematically; Logic and Proof; Use definitions, line, parallel line, and line segment based on the basic postulates, and theorems about points, undefined notions of point, line, distance along a line, ...
... 1. Know precise definitions of angle, circle, perpendicular C.1.a Using Logic and Proof to Reason Mathematically; Logic and Proof; Use definitions, line, parallel line, and line segment based on the basic postulates, and theorems about points, undefined notions of point, line, distance along a line, ...
Geometry Learning Targets Section Section Title Learning Targets I
... Find and Use Slopes of Lines 1. Find slope of a line given two points, graph 2. Classify lines given the slope ...
... Find and Use Slopes of Lines 1. Find slope of a line given two points, graph 2. Classify lines given the slope ...
Analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.Analytic geometry is widely used in physics and engineering, and is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.