Unit 4 Triangles - Clover Park School District
... Describe and apply the different types of transformations and be able to differentiate between them Perform translations, reflections, and rotations with and without the use of technology; including reflecting over parallel lines and reflecting over intersecting lines Describe and perform the compos ...
... Describe and apply the different types of transformations and be able to differentiate between them Perform translations, reflections, and rotations with and without the use of technology; including reflecting over parallel lines and reflecting over intersecting lines Describe and perform the compos ...
2015-2016 honors geometry curriculum map
... an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. ...
... an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. ...
answer key
... Standard: G.CO.2 – Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle measures to those that ...
... Standard: G.CO.2 – Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle measures to those that ...
geometry - Calculate
... Draw different views of prisms and solids formed from combinations of prisms (ACMMG161) Describe translations, reflections in an axis, and rotations of multiples of 90° on the Cartesian plane using Location and ...
... Draw different views of prisms and solids formed from combinations of prisms (ACMMG161) Describe translations, reflections in an axis, and rotations of multiples of 90° on the Cartesian plane using Location and ...
Geometry - Henrico County Public Schools
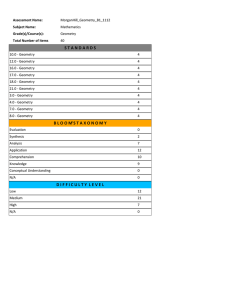
... Fill in the blank Hot spot Drag and drop Create a graph ...
... Fill in the blank Hot spot Drag and drop Create a graph ...
No Slide Title
... 4-7 Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
... 4-7 Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
Ag_mod05_les03 congruent parts of congruent triangles
... Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
... Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
Analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.Analytic geometry is widely used in physics and engineering, and is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.