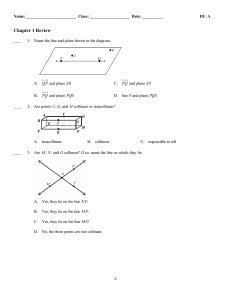
CONTENT BY STRAND - Houghton Mifflin Harcourt
... The Saxon Algebra 1, Geometry, and Algebra 2 series follows the Saxon pedagogy of incremental, integrated topics that distribute concepts across the year. This approach gives students time to master the abstract concepts needed to solve complex problems, and helps them to see the connectedness of ma ...
... The Saxon Algebra 1, Geometry, and Algebra 2 series follows the Saxon pedagogy of incremental, integrated topics that distribute concepts across the year. This approach gives students time to master the abstract concepts needed to solve complex problems, and helps them to see the connectedness of ma ...
GeometryPowerStandards Student Copy
... ● LT3: Construct a viable argument to justify a solution method. ● LT4: Identify pairs of angles as complementary, supplementary, adjacent, or vertical, and apply these relationships to determine missing angle measures ● LT5: Prove triangles congruent using SSS, SAS, ASA, AAS, and HL. Prove parts of ...
... ● LT3: Construct a viable argument to justify a solution method. ● LT4: Identify pairs of angles as complementary, supplementary, adjacent, or vertical, and apply these relationships to determine missing angle measures ● LT5: Prove triangles congruent using SSS, SAS, ASA, AAS, and HL. Prove parts of ...
Use coordinates to prove simple geometric theorems algebraically
... 2. Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translatio ...
... 2. Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translatio ...
Analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.Analytic geometry is widely used in physics and engineering, and is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.